cuBLAS
The API Reference guide for cuBLAS, the CUDA Basic Linear Algebra Subroutine library.
1. Introduction
The cuBLAS library is an implementation of BLAS (Basic Linear Algebra Subprograms) on top of the NVIDIA®CUDA™ runtime. It allows the user to access the computational resources of NVIDIA Graphics Processing Unit (GPU).
The cuBLAS Library exposes four sets of APIs:
The cuBLAS API, which is simply called cuBLAS API in this document (starting with CUDA 6.0),
The cuBLASXt API (starting with CUDA 6.0), and
The cuBLASLt API (starting with CUDA 10.1)
The cuBLASDx API (not shipped with the CUDA Toolkit)
To use the cuBLAS API, the application must allocate the required matrices and vectors in the GPU memory space, fill them with data, call the sequence of desired cuBLAS functions, and then upload the results from the GPU memory space back to the host. The cuBLAS API also provides helper functions for writing and retrieving data from the GPU.
To use the cuBLASXt API, the application may have the data on the Host or any of the devices involved in the computation, and the Library will take care of dispatching the operation to, and transferring the data to, one or multiple GPUs present in the system, depending on the user request.
The cuBLASLt is a lightweight library dedicated to GEneral Matrix-to-matrix Multiply (GEMM) operations with a new flexible API. This library adds flexibility in matrix data layouts, input types, compute types, and also in choosing the algorithmic implementations and heuristics through parameter programmability. After a set of options for the intended GEMM operation are identified by the user, these options can be used repeatedly for different inputs. This is analogous to how cuFFT and FFTW first create a plan and reuse for same size and type FFTs with different input data.
1.1. Data Layout
For maximum compatibility with existing Fortran environments, the cuBLAS library uses column-major storage, and 1-based indexing. Since C and C++ use row-major storage, applications written in these languages can not use the native array semantics for two-dimensional arrays. Instead, macros or inline functions should be defined to implement matrices on top of one-dimensional arrays. For Fortran code ported to C in mechanical fashion, one may chose to retain 1-based indexing to avoid the need to transform loops. In this case, the array index of a matrix element in row “i” and column “j” can be computed via the following macro
#define IDX2F(i,j,ld) ((((j)-1)*(ld))+((i)-1))
Here, ld refers to the leading dimension of the matrix, which in the case of column-major storage is the number of rows of the allocated matrix (even if only a submatrix of it is being used). For natively written C and C++ code, one would most likely choose 0-based indexing, in which case the array index of a matrix element in row “i” and column “j” can be computed via the following macro
#define IDX2C(i,j,ld) (((j)*(ld))+(i))
1.2. New and Legacy cuBLAS API
Starting with version 4.0, the cuBLAS Library provides a new API, in addition to the existing legacy API. This section discusses why a new API is provided, the advantages of using it, and the differences with the existing legacy API.
Warning
The legacy cuBLAS API is deprecated and will be removed in future release.
The new cuBLAS library API can be used by including the header file cublas_v2.h. It has the following features that the legacy cuBLAS API does not have:
The
handleto the cuBLAS library context is initialized using the function and is explicitly passed to every subsequent library function call. This allows the user to have more control over the library setup when using multiple host threads and multiple GPUs. This also allows the cuBLAS APIs to be reentrant.The scalars \(\alpha\) and \(\beta\) can be passed by reference on the host or the device, instead of only being allowed to be passed by value on the host. This change allows library functions to execute asynchronously using streams even when \(\alpha\) and \(\beta\) are generated by a previous kernel.
When a library routine returns a scalar result, it can be returned by reference on the host or the device, instead of only being allowed to be returned by value only on the host. This change allows library routines to be called asynchronously when the scalar result is generated and returned by reference on the device resulting in maximum parallelism.
The error status
cublasStatus_tis returned by all cuBLAS library function calls. This change facilitates debugging and simplifies software development. Note thatcublasStatuswas renamedcublasStatus_tto be more consistent with other types in the cuBLAS library.The
cublasAlloc()andcublasFree()functions have been deprecated. This change removes these unnecessary wrappers aroundcudaMalloc()andcudaFree(), respectively.The function
cublasSetKernelStream()was renamedcublasSetStream()to be more consistent with the other CUDA libraries.
The legacy cuBLAS API, explained in more detail in Using the cuBLAS Legacy API, can be used by including the header file cublas.h. Since the legacy API is identical to the previously released cuBLAS library API, existing applications will work out of the box and automatically use this legacy API without any source code changes.
The current and the legacy cuBLAS APIs cannot be used simultaneously in a single translation unit: including both cublas.h and cublas_v2.h header files will lead to compilation errors due to incompatible symbol redeclarations.
In general, new applications should not use the legacy cuBLAS API, and existing applications should convert to using the new API if it requires sophisticated and optimal stream parallelism, or if it calls cuBLAS routines concurrently from multiple threads.
For the rest of the document, the new cuBLAS Library API will simply be referred to as the cuBLAS Library API.
As mentioned earlier the interfaces to the legacy and the cuBLAS library APIs are the header file cublas.h and cublas_v2.h, respectively. In addition, applications using the cuBLAS library need to link against:
The DSO
cublas.sofor Linux,The DLL
cublas.dllfor Windows, orThe dynamic library
cublas.dylibfor Mac OS X.
Note
The same dynamic library implements both the new and legacy cuBLAS APIs.
1.3. Example Code
For sample code references please see the two examples below. They show an application written in C using the cuBLAS library API with two indexing styles (Example 1. “Application Using C and cuBLAS: 1-based indexing” and Example 2. “Application Using C and cuBLAS: 0-based Indexing”).
//Example 1. Application Using C and cuBLAS: 1-based indexing
//-----------------------------------------------------------
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <cuda_runtime.h>
#include "cublas_v2.h"
#define M 6
#define N 5
#define IDX2F(i,j,ld) ((((j)-1)*(ld))+((i)-1))
static __inline__ void modify (cublasHandle_t handle, float *m, int ldm, int n, int p, int q, float alpha, float beta){
cublasSscal (handle, n-q+1, &alpha, &m[IDX2F(p,q,ldm)], ldm);
cublasSscal (handle, ldm-p+1, &beta, &m[IDX2F(p,q,ldm)], 1);
}
int main (void){
cudaError_t cudaStat;
cublasStatus_t stat;
cublasHandle_t handle;
int i, j;
float* devPtrA;
float* a = 0;
a = (float *)malloc (M * N * sizeof (*a));
if (!a) {
printf ("host memory allocation failed");
return EXIT_FAILURE;
}
for (j = 1; j <= N; j++) {
for (i = 1; i <= M; i++) {
a[IDX2F(i,j,M)] = (float)((i-1) * N + j);
}
}
cudaStat = cudaMalloc ((void**)&devPtrA, M*N*sizeof(*a));
if (cudaStat != cudaSuccess) {
printf ("device memory allocation failed");
free (a);
return EXIT_FAILURE;
}
stat = cublasCreate(&handle);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("CUBLAS initialization failed\n");
free (a);
cudaFree (devPtrA);
return EXIT_FAILURE;
}
stat = cublasSetMatrix (M, N, sizeof(*a), a, M, devPtrA, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data download failed");
free (a);
cudaFree (devPtrA);
cublasDestroy(handle);
return EXIT_FAILURE;
}
modify (handle, devPtrA, M, N, 2, 3, 16.0f, 12.0f);
stat = cublasGetMatrix (M, N, sizeof(*a), devPtrA, M, a, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data upload failed");
free (a);
cudaFree (devPtrA);
cublasDestroy(handle);
return EXIT_FAILURE;
}
cudaFree (devPtrA);
cublasDestroy(handle);
for (j = 1; j <= N; j++) {
for (i = 1; i <= M; i++) {
printf ("%7.0f", a[IDX2F(i,j,M)]);
}
printf ("\n");
}
free(a);
return EXIT_SUCCESS;
}
//Example 2. Application Using C and cuBLAS: 0-based indexing
//-----------------------------------------------------------
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <cuda_runtime.h>
#include "cublas_v2.h"
#define M 6
#define N 5
#define IDX2C(i,j,ld) (((j)*(ld))+(i))
static __inline__ void modify (cublasHandle_t handle, float *m, int ldm, int n, int p, int q, float alpha, float beta){
cublasSscal (handle, n-q, &alpha, &m[IDX2C(p,q,ldm)], ldm);
cublasSscal (handle, ldm-p, &beta, &m[IDX2C(p,q,ldm)], 1);
}
int main (void){
cudaError_t cudaStat;
cublasStatus_t stat;
cublasHandle_t handle;
int i, j;
float* devPtrA;
float* a = 0;
a = (float *)malloc (M * N * sizeof (*a));
if (!a) {
printf ("host memory allocation failed");
return EXIT_FAILURE;
}
for (j = 0; j < N; j++) {
for (i = 0; i < M; i++) {
a[IDX2C(i,j,M)] = (float)(i * N + j + 1);
}
}
cudaStat = cudaMalloc ((void**)&devPtrA, M*N*sizeof(*a));
if (cudaStat != cudaSuccess) {
printf ("device memory allocation failed");
free (a);
return EXIT_FAILURE;
}
stat = cublasCreate(&handle);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("CUBLAS initialization failed\n");
free (a);
cudaFree (devPtrA);
return EXIT_FAILURE;
}
stat = cublasSetMatrix (M, N, sizeof(*a), a, M, devPtrA, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data download failed");
free (a);
cudaFree (devPtrA);
cublasDestroy(handle);
return EXIT_FAILURE;
}
modify (handle, devPtrA, M, N, 1, 2, 16.0f, 12.0f);
stat = cublasGetMatrix (M, N, sizeof(*a), devPtrA, M, a, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data upload failed");
free (a);
cudaFree (devPtrA);
cublasDestroy(handle);
return EXIT_FAILURE;
}
cudaFree (devPtrA);
cublasDestroy(handle);
for (j = 0; j < N; j++) {
for (i = 0; i < M; i++) {
printf ("%7.0f", a[IDX2C(i,j,M)]);
}
printf ("\n");
}
free(a);
return EXIT_SUCCESS;
}
1.4. Forward Compatibility
cuBLAS library can work on future GPUs in most cases thanks to PTX JIT. However, there are certain limitations:
There are no performance guarantees: running on new hardware may be slower despite better theoretical peaks.
There is limited forward compatibility for narrow precisions (FP4 and FP8) and tiled 8-bit integer layouts.
1.5. Floating Point Emulation
Floating point emulation was first introduced in CUDA 12.9 and is used to further accelerate matrix multiplication for higher precision data types. Floating point emulation works by first transforming the inputs into multiple lower precision values, then leverages lower precision hardware units to compute partial results, and finally recombines the results back into full precision. These algorithms can provide a significant performance advantage over native precision arithmetic while maintaining the same or better accuracy; however, the results are not IEEE-754 compliant.
Floating Point Emulation Algorithm |
Precision Emulated |
Supported compute capabilities |
CUDA Version |
|---|---|---|---|
FP32 |
10.0, 10.3 |
12.9+ |
|
FP64 |
8.x, 9.0, 10.0, 11.0, 12.x |
13.0u2+ |
To enable floating point emulation without any code changes, the following environment variables can be used.
Environment Variable |
Description |
|---|---|
|
An environment variable for overriding the default emulation strategy. The valid values are |
|
An environment variable for enabling and disabling single precision floating point emulation using the values 1 and 0, respectively. |
|
An environment variable for enabling and disabling double precision floating point emulation using the values 1 and 0, respectively. |
|
The number of mantissa bits to be used for fixed-point emulation. When set, emulated algorithms will use the specified number of mantissa bits. This is equivalent to calling cublasSetFixedPointEmulationMantissaControl() with |
1.5.1. BF16x9
The BF16x9 algorithm is used for emulating FP32 arithmetic. An FP32 value can be exactly represented as three BF16 values as follows:
We can fully reconstruct the FP32 value from the BF16 values without any loss of accuracy. Using this, we define an FMA operation (d = ab + c) as follows:
In practice, the BF16 tensor cores are utilized rather than FMA units and this idea naturally extends into complex arithmetic as well.
While BF16x9 can be supported on all hardware, it only provides a performance advantage when peak BF16 throughput is more than nine times greater than peak FP32 throughput. It also requires special hardware features to apply the additional scaling factors in a performant manner. As a result, BF16x9 is only supported on select architectures. See the Floating Point Emulation Support Overview table for more details.
1.5.2. Fixed-Point
Fixed-point emulation is used for emulating FP64 arithmetic and follows the Ozaki Scheme. Fixed-point representations emulate floating point through the addition of a shared power of two scaling factor and by encoding the remaining dynamic range of floating point within mantissa bits. The scaling factor is shared for elements in the same row of the A matrix or column of the B matrix and is used to logically scale all elements to be between -1 and 1 inclusively.
Due to the large dynamic range of FP64, there is no single configuration of fixed-point which is both performant and accurate for all floating point inputs. Therefore, we enable two flavors of fixed-point emulation: Dynamic Mantissa Control and Fixed Mantissa Control. These configurations can be set with cublasSetFixedPointEmulationMantissaControl().
1.5.2.1. Dynamic Mantissa Control
Dynamic mantissa control represents the cuBLAS library default mantissa control. Our automatic dynamic precision framework computes the proper number of fixed-point mantissa bits required to maintain equal or better accuracy than FP64. If the number of required mantissa bits exceeds a library defined default (see Default Library Configurations) or a user provided maximum number of bits (see cublasSetFixedPointEmulationMaxMantissaBitCount()), the framework dynamically dispatches to native FP64.
1.5.2.2. Fixed Mantissa Control
Fixed mantissa control can be leveraged to further accelerate fixed-point emulation. The user can provide the number of mantissa bits for the fixed-point representation via cublasSetFixedPointEmulationMaxMantissaBitCount(); however, without the automatic dynamic precision framework, it is not possible to guarantee equal or better accuracy than FP64 arithmetic.
1.5.2.3. Representation and Mappings
The fixed-point representation consists of a shared scaling factor for elements in the same row or column of a matrix, a sign bit, and mantissa bits. We store the sign bit and mantissa bits within 8-bit integers. Each matrix of 8-bit integers are referred to as a slice and the computational cost grows quadratically with the number of slices. The formula to convert mantissa bit count to slice count is as follows:
Note
The number of mantissa bits will always be rounded up to fully occupy the least significant slice
1.5.2.4. Fixed-Point Workspace Requirements
To compute with fixed-point emulation, the A and B matrices are translated into a fixed-point representation in workspace memory. This leads to workspace requirements that are problem size and emulation parameter dependent. The following function will provide a safe bound (possibly overestimating) on the workspace required for fixed-point emulation:
size_t getFixedPointWorkspaceSizeInBytes(int m, int n, int k, int batchCount, bool isComplex,
cudaEmulationMantissaControl mantissaControl, int maxMantissaBitCount) {
constexpr double MULTIPLIER = 1.25;
int mult = isComplex ? 2 : 1;
int numSlices = ceildiv(maxMantissaBitCount + 1, 8);
int padded_m = ceildiv(m, 1024) * 1024;
int padded_n = ceildiv(n, 1024) * 1024;
int padded_k = ceildiv(k, 128) * 128;
int num_blocks_k = ceildiv(k, 64);
size_t gemm_workspace = sizeof(int8_t) *
((size_t)padded_m * padded_k + (size_t)padded_n * padded_k) * mult * numSlices;
gemm_workspace += sizeof(int32_t) * ((size_t)padded_m + padded_n) * mult;
if (isComplex) {
gemm_workspace += sizeof(double) * (size_t)m * n * mult * mult;
}
size_t adp_workspace = 0;
if (mantissaControl == CUDA_EMULATION_MANTISSA_CONTROL_DYNAMIC) {
adp_workspace = sizeof(int32_t) * ((size_t)m * num_blocks_k + (size_t)n * num_blocks_k +
(size_t)m * n) * mult;
}
constexpr size_t CONSTANT_SIZE = 128 * 1024 * 1024;
return (size_t)(std::max(gemm_workspace, adp_workspace) * batchCount * MULTIPLIER) + CONSTANT_SIZE;
}
This function can be used to manage your own workspace memory with cublasSetWorkspace(), which can be used to guarantee reproducible results and improve performance.
1.5.2.5. Fixed-Point Performance Guide
Fixed-point emulation allows users to make performance and precision trade-offs for further acceleration. For dynamic mantissa control, users are able to configure the automatic dynamic precision framework to use fewer or more bits than the accuracy of native FP64 requires with cublasSetFixedPointEmulationMantissaBitOffset(). Fixed mantissa control can be similarly tuned by increasing or decreasing the number of mantissa bits with cublasSetFixedPointEmulationMaxMantissaBitCount().
Due to the large fixed-point workspace requirements, asynchronous allocation is done with cudaMallocAsync(). In cases where not enough GEMMs are called to amortize the cost of memory allocation, or very frequent CUDA stream synchronization occurs, you can improve performance by:
Reducing the number of CUDA stream synchronizations
Managing your own memory and providing workspace with cublasSetWorkspace()
Allowing the default memory pool to retain memory between synchronizations
1.5.3. Default Library Configurations
Library default values for emulation are subject to change.
API |
Mantissa Control |
Default Behavior |
|---|---|---|
Not applicable |
|
|
Not applicable |
|
|
Not applicable |
|
|
CUDA_EMULATION_MANTISSA_CONTROL_DYNAMIC |
79 |
|
CUDA_EMULATION_MANTISSA_CONTROL_FIXED |
55 |
|
Not applicable |
0 |
|
Not applicable |
NULL |
1.5.4. Support For Floating Point Special Values
The implementations of floating point emulation algorithms maintain the accuracy of the emulated precision for both normal and denormalized values but may not adhere to the IEEE-754 standard with respect to \(\text{Inf}\), \(\text{NaN}\), or signed zeros. If the underlying emulated algorithm cannot implicitly support a given special value, and the library is configured to support it (see cublasSetEmulationSpecialValuesSupport()), then extra steps are taken to support it. The following table shows which special values are implicitly supported for each emulation algorithm.
Floating Point Emulation Algorithm |
Implicitly Supported Special Values |
|---|---|
\(\text{NaN}\) |
|
None |
2. Using the cuBLAS API
2.1. General Description
This section describes how to use the cuBLAS library API.
2.1.1. Error Status
All cuBLAS library function calls return the error status cublasStatus_t.
2.1.2. cuBLAS Context
The application must initialize a handle to the cuBLAS library context by calling the cublasCreate() function. Then, the handle is explicitly passed to every subsequent library function call. Once the application finishes using the library, it must call the function cublasDestroy() to release the resources associated with the cuBLAS library context.
This approach allows the user to explicitly control the library setup when using multiple host threads and multiple GPUs. For example, the application can use cudaSetDevice() to associate different devices with different host threads and in each of those host threads it can initialize a unique handle to the cuBLAS library context, which will use the particular device associated with that host thread. Then, the cuBLAS library function calls made with different handles will automatically dispatch the computation to different devices.
The device associated with a particular cuBLAS context is assumed to remain unchanged between the corresponding cublasCreate() and cublasDestroy() calls. In order for the cuBLAS library to use a different device in the same host thread, the application must set the new device to be used by calling cudaSetDevice() and then create another cuBLAS context, which will be associated with the new device, by calling cublasCreate(). When multiple devices are available, applications must ensure that the device associated with a given cuBLAS context is current (e.g. by calling cudaSetDevice()) before invoking cuBLAS functions with this context.
A cuBLAS library context is tightly coupled with the CUDA context that is current at the time of the cublasCreate() call. An application that uses multiple CUDA contexts is required to create a cuBLAS context per CUDA context and make sure the former never outlives the latter. Starting from version 12.8, cuBLAS detects if the underlying CUDA context is tied to a graphics context and follows the shared memory size limits that are set in such case.
2.1.3. Thread Safety
The library is thread safe and its functions can be called from multiple host threads, even with the same handle. When multiple threads share the same handle, extreme care needs to be taken when the handle configuration is changed because that change will affect potentially subsequent cuBLAS calls in all threads. It is even more true for the destruction of the handle. So it is not recommended that multiple thread share the same cuBLAS handle.
Additional considerations apply when the same handle is used from multiple threads with a user provided workspace. See cublasSetWorkspace() for details.
2.1.4. Results Reproducibility
By design, all cuBLAS API routines from a given toolkit version, generate the same bit-wise results at every run when executed on GPUs with the same architecture and the same number of SMs. However, bit-wise reproducibility is not guaranteed across toolkit versions because the implementation might differ due to some implementation changes.
This guarantee no longer holds when multiple CUDA streams are active or fixed-point emulation is used. If multiple concurrent streams are active, the library may optimize total performance by picking different internal implementations.
Note
The non-deterministic behavior of multi-stream execution is due to library optimizations in selecting internal workspace for the routines running in parallel streams. To avoid this effect user can either:
provide a separate workspace for each used stream using the cublasSetWorkspace() function, or
have one cuBLAS handle per stream, or
use cublasLtMatmul() instead of GEMM-family of functions and provide user owned workspace, or
set a debug environment variable
CUBLAS_WORKSPACE_CONFIGto:16:8(may limit overall performance) or:4096:8(will increase library footprint in GPU memory by approximately 24MiB).
The non-deterministic behavior of fixed-point emulation is due to the large workspace memory requirements (see Fixed-Point Workspace Requirements for details). This requires dynamically allocating memory with cudaMallocAsync() and allocation failures result in fallbacks to non-emulated routines. To avoid this effect, users can provide workspace via cublasSetWorkspace() to meet fixed-point emulation workspace requirements.
Any of those settings will allow for deterministic behavior even with multiple concurrent streams sharing a single cuBLAS handle.
This behavior is expected to change in a future release.
For some routines such as cublas<t>symv() and cublas<t>hemv(), an alternate significantly faster routine can be chosen using the routine cublasSetAtomicsMode(). In that case, the results are not guaranteed to be bit-wise reproducible because atomics are used for the computation.
2.1.5. Scalar Parameters
There are two categories of the functions that use scalar parameters :
Functions that take
alphaand/orbetaparameters by reference on the host or the device as scaling factors, such asgemm.Functions that return a scalar result on the host or the device such as
amax(),amin,asum(),rotg(),rotmg(),dot()andnrm2().
For the functions of the first category, when the pointer mode is set to CUBLAS_POINTER_MODE_HOST, the scalar parameters alpha and/or beta can be on the stack or allocated on the heap, shouldn’t be placed in managed memory. Underneath, the CUDA kernels related to those functions will be launched with the value of alpha and/or beta. Therefore if they were allocated on the heap, they can be freed just after the return of the call even though the kernel launch is asynchronous. When the pointer mode is set to CUBLAS_POINTER_MODE_DEVICE, alpha and/or beta must be accessible on the device and their values should not be modified until the kernel is done. Note that since cudaFree() does an implicit cudaDeviceSynchronize(), cudaFree() can still be called on alpha and/or beta just after the call but it would defeat the purpose of using this pointer mode in that case.
For the functions of the second category, when the pointer mode is set to CUBLAS_POINTER_MODE_HOST, these functions block the CPU, until the GPU has completed its computation and the results have been copied back to the Host. When the pointer mode is set to CUBLAS_POINTER_MODE_DEVICE, these functions return immediately. In this case, similar to matrix and vector results, the scalar result is ready only when execution of the routine on the GPU has completed. This requires proper synchronization in order to read the result from the host.
In either case, the pointer mode CUBLAS_POINTER_MODE_DEVICE allows the library functions to execute completely asynchronously from the Host even when alpha and/or beta are generated by a previous kernel. For example, this situation can arise when iterative methods for solution of linear systems and eigenvalue problems are implemented using the cuBLAS library.
2.1.6. Parallelism with Streams
If the application uses the results computed by multiple independent tasks, CUDA™ streams can be used to overlap the computation performed in these tasks.
The application can conceptually associate each stream with each task. In order to achieve the overlap of computation between the tasks, the user should create CUDA™ streams using the function cudaStreamCreate() and set the stream to be used by each individual cuBLAS library routine by calling cublasSetStream() just before calling the actual cuBLAS routine. Note that cublasSetStream() resets the user-provided workspace to the default workspace pool; see cublasSetWorkspace(). Then, the computation performed in separate streams would be overlapped automatically when possible on the GPU. This approach is especially useful when the computation performed by a single task is relatively small and is not enough to fill the GPU with work.
We recommend using the new cuBLAS API with scalar parameters and results passed by reference in the device memory to achieve maximum overlap of the computation when using streams.
A particular application of streams, batching of multiple small kernels, is described in the following section.
2.1.7. Batching Kernels
In this section, we explain how to use streams to batch the execution of small kernels. For instance, suppose that we have an application where we need to make many small independent matrix-matrix multiplications with dense matrices.
It is clear that even with millions of small independent matrices we will not be able to achieve the same GFLOPS rate as with a one large matrix. For example, a single \(n \times n\) large matrix-matrix multiplication performs \(n^{3}\) operations for \(n^{2}\) input size, while 1024 \(\frac{n}{32} \times \frac{n}{32}\) small matrix-matrix multiplications perform \(1024\left( \frac{n}{32} \right)^{3} = \frac{n^{3}}{32}\) operations for the same input size. However, it is also clear that we can achieve a significantly better performance with many small independent matrices compared with a single small matrix.
The architecture family of GPUs allows us to execute multiple kernels simultaneously. Hence, in order to batch the execution of independent kernels, we can run each of them in a separate stream. In particular, in the above example we could create 1024 CUDA™ streams using the function cudaStreamCreate(), then preface each call to cublas<t>gemm() with a call to cublasSetStream() with a different stream for each of the matrix-matrix multiplications (note that cublasSetStream() resets user-provided workspace to the default workspace pool, see cublasSetWorkspace()). This will ensure that when possible the different computations will be executed concurrently. Although the user can create many streams, in practice it is not possible to have more than 32 concurrent kernels executing at the same time.
2.1.8. Cache Configuration
On some devices, L1 cache and shared memory use the same hardware resources. The cache configuration can be set directly with the CUDA Runtime function cudaDeviceSetCacheConfig. The cache configuration can also be set specifically for some functions using the routine cudaFuncSetCacheConfig. Please refer to the CUDA Runtime API documentation for details about the cache configuration settings.
Because switching from one configuration to another can affect kernels concurrency, the cuBLAS Library does not set any cache configuration preference and relies on the current setting. However, some cuBLAS routines, especially Level-3 routines, rely heavily on shared memory. Thus the cache preference setting might affect adversely their performance.
2.1.9. Static Library Support
The cuBLAS Library is also delivered in a static form as libcublas_static.a on Linux. The static cuBLAS library and all other static math libraries depend on a common thread abstraction layer library called libculibos.a.
For example, on Linux, to compile a small application using cuBLAS, against the dynamic library, the following command can be used:
nvcc myCublasApp.c -lcublas -o myCublasApp
Whereas to compile against the static cuBLAS library, the following command must be used:
nvcc myCublasApp.c -lcublas_static -lculibos -o myCublasApp
It is also possible to use the native Host C++ compiler. Depending on the Host operating system, some additional libraries like pthread or dl might be needed on the linking line. The following command on Linux is suggested :
g++ myCublasApp.c -lcublas_static -lculibos -lcudart_static -lpthread -ldl -I <cuda-toolkit-path>/include -L <cuda-toolkit-path>/lib64 -o myCublasApp
Note that in the latter case, the library cuda is not needed. The CUDA Runtime will try to open explicitly the cuda library if needed. In the case of a system which does not have the CUDA driver installed, this allows the application to gracefully manage this issue and potentially run if a CPU-only path is available.
Starting with release 11.2, using the typed functions instead of the extension functions (cublas**Ex()) helps in reducing the binary size when linking to static cuBLAS Library.
2.1.10. GEMM Algorithms Numerical Behavior
Some GEMM algorithms split the computation along the dimension K to increase the GPU occupancy, especially when the dimension K is large compared to dimensions M and N. When this type of algorithm is chosen by the cuBLAS heuristics or explicitly by the user, the results of each split is summed deterministically into the resulting matrix to get the final result.
For the routines cublas<t>gemmEx() and cublasGemmEx(), when the compute type is greater than the output type, the sum of the split chunks can potentially lead to some intermediate overflows thus producing a final resulting matrix with some overflows. Those overflows might not have occurred if all the dot products had been accumulated in the compute type before being converted at the end in the output type. This computation side-effect can be easily exposed when the computeType is CUDA_R_32F and Atype, Btype and Ctype are CUDA_R_16F. This behavior can be controlled using the compute precision mode CUBLAS_MATH_DISALLOW_REDUCED_PRECISION_REDUCTION with cublasSetMathMode()
2.1.11. Tensor Core Usage
Tensor cores were first introduced with Volta GPUs (compute capability 7.0 and above) and significantly accelerate matrix multiplications. Starting with cuBLAS version 11.0.0, the library may automatically make use of Tensor Core capabilities wherever possible, unless they are explicitly disabled by selecting pedantic compute modes in cuBLAS (see cublasSetMathMode(), cublasMath_t).
It should be noted that the library will pick a Tensor Core enabled implementation wherever it determines that it would provide the best performance.
The best performance when using Tensor Cores can be achieved when the matrix dimensions and pointers meet certain memory alignment requirements. Specifically, all of the following conditions must be satisfied to get the most performance out of Tensor Cores:
((op_A == CUBLAS_OP_N ? m : k) * AtypeSize) % 16 == 0((op_B == CUBLAS_OP_N ? k : n) * BtypeSize) % 16 == 0(m * CtypeSize) % 16 == 0(lda * AtypeSize) % 16 == 0(ldb * BtypeSize) % 16 == 0(ldc * CtypeSize) % 16 == 0intptr_t(A) % 16 == 0intptr_t(B) % 16 == 0intptr_t(C) % 16 == 0
To conduct matrix multiplication with FP8 types (see 8-bit Floating Point Data Types (FP8) Usage), you must ensure that your matrix dimensions and pointers meet the optimal requirements listed above. Aside from FP8, there are no longer any restrictions on matrix dimensions and memory alignments to use Tensor Cores (starting with cuBLAS version 11.0.0).
2.1.12. CUDA Graphs Support
cuBLAS routines can be captured in CUDA Graph stream capture without restrictions in most situations.
The exception are routines that output results into host buffers (e.g. cublas<t>dot() while pointer mode CUBLAS_POINTER_MODE_HOST is configured), as it enforces synchronization.
For input coefficients (such as alpha, beta) behavior depends on the pointer mode setting:
In the case of
CUBLAS(LT)_POINTER_MODE_HOST, coefficient values are captured in the graph.In the case of pointer modes with device pointers, coefficient value is accessed using the device pointer at the time of graph execution.
Note
When captured in CUDA Graph stream capture, cuBLAS routines can create memory nodes through the use of stream-ordered allocation APIs, cudaMallocAsync and cudaFreeAsync. However, as there is currently no support for memory nodes in child graphs or graphs launched from the device, attempts to capture cuBLAS routines in such scenarios may fail. To avoid this issue, use the cublasSetWorkspace() function to provide user-owned workspace memory.
2.1.13. 64-bit Integer Interface
cuBLAS version 12 introduced 64-bit integer capable functions. Each 64-bit integer function is equivalent to a 32-bit integer function with the following changes:
The function name has
_64suffix.The dimension (problem size) data type changed from
inttoint64_t. Examples of dimension:m,n, andk.The leading dimension data type changed from
inttoint64_t. Examples of leading dimension:lda,ldb, andldc.The vector increment data type changed from
inttoint64_t. Examples of vector increment:incxandincy.
For example, consider the following 32-bit integer functions:
cublasStatus_t cublasSetMatrix(int rows, int cols, int elemSize, const void *A, int lda, void *B, int ldb);
cublasStatus_t cublasIsamax(cublasHandle_t handle, int n, const float *x, int incx, int *result);
cublasStatus_t cublasSsyr(cublasHandle_t handle, cublasFillMode_t uplo, int n, const float *alpha, const float *x, int incx, float *A, int lda);
The equivalent 64-bit integer functions are:
cublasStatus_t cublasSetMatrix_64(int64_t rows, int64_t cols, int64_t elemSize, const void *A, int64_t lda, void *B, int64_t ldb);
cublasStatus_t cublasIsamax_64(cublasHandle_t handle, int64_t n, const float *x, int64_t incx, int64_t *result);
cublasStatus_t cublasSsyr_64(cublasHandle_t handle, cublasFillMode_t uplo, int64_t n, const float *alpha, const float *x, int64_t incx, float *A, int64_t lda);
Not every function has a 64-bit integer equivalent. For instance, cublasSetMathMode() doesn’t have any arguments that could meaningfully be int64_t. For documentation brevity, the 64-bit integer APIs are not explicitly listed, but only mentioned that they exist for the relevant functions.
2.2. cuBLAS Datatypes Reference
2.2.1. cublasHandle_t
The cublasHandle_t type is a pointer type to an opaque structure holding the cuBLAS library context. The cuBLAS library context must be initialized using cublasCreate() and the returned handle must be passed to all subsequent library function calls. The context should be destroyed at the end using cublasDestroy().
2.2.2. cublasStatus_t
The type is used for function status returns. All cuBLAS library functions return their status, which can have the following values.
Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The cuBLAS library was not initialized. This is usually caused by the lack of a prior cublasCreate() call, an error in the CUDA Runtime API called by the cuBLAS routine, or an error in the hardware setup. To correct: call cublasCreate() before the function call; and check that the hardware, an appropriate version of the driver, and the cuBLAS library are correctly installed. |
|
Resource allocation failed inside the cuBLAS library. This is usually caused by a To correct: prior to the function call, deallocate previously allocated memory as much as possible. |
|
An unsupported value or parameter was passed to the function (a negative vector size, for example). To correct: ensure that all the parameters being passed have valid values. |
|
The function requires a feature absent from the device architecture; usually caused by compute capability lower than 5.0. To correct: compile and run the application on a device with appropriate compute capability. |
|
An access to GPU memory space failed, which is usually caused by a failure to bind a texture. To correct: before the function call, unbind any previously bound textures. |
|
The GPU program failed to execute. This is often caused by a launch failure of the kernel on the GPU, which can be caused by multiple reasons. To correct: check that the hardware, an appropriate version of the driver, and the cuBLAS library are correctly installed. |
|
An internal cuBLAS operation failed. This error is usually caused by a To correct: check that the hardware, an appropriate version of the driver, and the cuBLAS library are correctly installed. Also, check that the memory passed as a parameter to the routine is not being deallocated prior to the routine’s completion. |
|
The functionality requested is not supported. |
|
The functionality requested requires some license and an error was detected when trying to check the current licensing. This error can happen if the license is not present or is expired or if the environment variable NVIDIA_LICENSE_FILE is not set properly. |
2.2.3. cublasOperation_t
The cublasOperation_t type indicates which operation needs to be performed with the dense matrix. Its values correspond to Fortran characters ‘N’ or ‘n’ (non-transpose), ‘T’ or ‘t’ (transpose) and ‘C’ or ‘c’ (conjugate transpose) that are often used as parameters to legacy BLAS implementations.
Value |
Meaning |
|---|---|
|
The non-transpose operation is selected. |
|
The transpose operation is selected. |
|
The conjugate transpose operation is selected. |
2.2.4. cublasFillMode_t
The type indicates which part (lower or upper) of the dense matrix was filled and consequently should be used by the function. Its values correspond to Fortran characters L or l (lower) and U or u (upper) that are often used as parameters to legacy BLAS implementations.
Value |
Meaning |
|---|---|
|
The lower part of the matrix is filled. |
|
The upper part of the matrix is filled. |
|
The full matrix is filled. |
2.2.5. cublasDiagType_t
The type indicates whether the main diagonal of the dense matrix is unity and consequently should not be touched or modified by the function. Its values correspond to Fortran characters ‘N’ or ‘n’ (non-unit) and ‘U’ or ‘u’ (unit) that are often used as parameters to legacy BLAS implementations.
Value |
Meaning |
|---|---|
|
The matrix diagonal has non-unit elements. |
|
The matrix diagonal has unit elements. |
2.2.6. cublasSideMode_t
The type indicates whether the dense matrix is on the left or right side in the matrix equation solved by a particular function. Its values correspond to Fortran characters ‘L’ or ‘l’ (left) and ‘R’ or ‘r’ (right) that are often used as parameters to legacy BLAS implementations.
Value |
Meaning |
|---|---|
|
The matrix is on the left side in the equation. |
|
The matrix is on the right side in the equation. |
2.2.7. cublasPointerMode_t
The cublasPointerMode_t type indicates whether the scalar values are passed by reference on the host or device. It is important to point out that if several scalar values are present in the function call, all of them must conform to the same single pointer mode. The pointer mode can be set and retrieved using cublasSetPointerMode() and cublasGetPointerMode() routines, respectively.
Value |
Meaning |
|---|---|
|
The scalars are passed by reference on the host. |
|
The scalars are passed by reference on the device. |
2.2.8. cublasAtomicsMode_t
The type indicates whether cuBLAS routines which has an alternate implementation using atomics can be used. The atomics mode can be set and queried using cublasSetAtomicsMode() and cublasGetAtomicsMode() and routines, respectively.
Value |
Meaning |
|---|---|
|
The usage of atomics is not allowed. |
|
The usage of atomics is allowed. |
2.2.9. cublasGemmAlgo_t
cublasGemmAlgo_t type is an enumerant to specify the algorithm for matrix-matrix multiplication on GPU architectures up to sm_75. On sm_80 and newer GPU architectures, this enumarant has no effect. cuBLAS has the following algorithm options:
Value |
Meaning |
|---|---|
|
Apply Heuristics to select the GEMM algorithm |
|
Explicitly choose an Algorithm |
|
This mode is deprecated and will be removed in a future release. Apply Heuristics to select the GEMM algorithm, while allowing use of reduced precision CUBLAS_COMPUTE_32F_FAST_16F kernels (for backward compatibility). |
|
Those values are deprecated and will be removed in a future release. Explicitly choose a Tensor core GEMM Algorithm |
|
[EXPERIMENTAL] The library will benchmark a number of available algorithms and choose the optimal one for the given problem configuration. Solution is cached in cublas handle so that next calls with the problem size will use the cached configuration. Note: To avoid overwriting the user’s data, the library will allocate the amount of memory corresponding to the size of the output. Note: The benchmarking is not supported during stream capture; CUBLAS_STATUS_NOT_SUPPORTED will be returned under stream capture if no configuration was found in the cache for the given problem size. |
2.2.10. cublasMath_t
cublasMath_t enumerate type is used in cublasSetMathMode() to choose compute precision modes as defined in the following table. Since this setting does not directly control the use of Tensor Cores, the mode CUBLAS_TENSOR_OP_MATH is being deprecated, and will be removed in a future release.
Value |
Meaning |
|---|---|
|
This is the default and highest-performance mode that uses compute and intermediate storage precisions with at least the same number of mantissa and exponent bits as requested. Tensor Cores will be used whenever possible. |
|
This mode uses the prescribed precision and standardized arithmetic for all phases of calculations and is primarily intended for numerical robustness studies, testing, and debugging. This mode might not be as performant as the other modes. |
|
Enable acceleration of single-precision routines using TF32 tensor cores. Note that input conversions round to nearest even. |
|
Enable acceleration of single-precision routines using the BF16x9 algorithm. See Floating Point Emulation for more details. For single precision GEMM routines cuBLAS will use the |
|
Enable acceleration of double-precision routines using fixed-point emulation algorithms. See Floating Point Emulation for more details. |
|
Forces any reductions during matrix multiplications to use the accumulator type (that is, compute type) and not the output type in case of mixed precision routines where output type precision is less than the compute type precision. This is a flag that can be set (using a bitwise or operation) alongside any of the other values. |
|
This mode is deprecated and will be removed in a future release. Allows the library to use Tensor Core operations whenever possible. For single precision GEMM routines cuBLAS will use the |
2.2.11. cublasComputeType_t
cublasComputeType_t enumerate type is used in cublasGemmEx() and cublasLtMatmul() (including all batched and strided batched variants) to choose compute precision modes as defined below.
Value | Meaning |
||
|---|---|---|
|
This is the default and highest-performance mode for 16-bit half precision floating point and all compute and intermediate storage precisions with at least 16-bit half precision. Tensor Cores will be used whenever possible. |
|
|
This mode uses 16-bit half precision floating point standardized arithmetic for all phases of calculations and is primarily intended for numerical robustness studies, testing, and debugging. This mode might not be as performant as the other modes since it disables use of tensor cores. |
|
|
This is the default 32-bit single precision floating point and uses compute and intermediate storage precisions of at least 32-bits. |
|
|
Uses 32-bit single precision floating point arithmetic for all phases of calculations and also disables algorithmic optimizations such as Gaussian complexity reduction (3M). |
|
|
Allows the library to use Tensor Cores with automatic down-conversion and 16-bit half-precision compute for 32-bit input and output matrices. |
|
|
Allows the library to use Tensor Cores with automatic down-convesion and bfloat16 compute for 32-bit input and output matrices. See Alternate Floating Point section for more details on bfloat16. |
|
|
Allows the library to use Tensor Cores with TF32 compute for 32-bit floating point input and output matrices. Note that input conversions round to nearest even. See Alternate Floating Point section for more details on TF32 compute. |
|
|
Allows the library to use the BF16x9 floating point emulation algorithm for 32-bit floating point arithmetic. See Floating Point Emulation for more details. |
|
|
This is the default 64-bit double precision floating point and uses compute and intermediate storage precisions of at least 64-bits. |
|
|
Allows the library to use fixed-point emulation algorithms for 64-bit double precision floating point arithmetic. See Floating Point Emulation for more details. |
|
|
Uses 64-bit double precision floating point arithmetic for all phases of calculations and also disables algorithmic optimizations such as Gaussian complexity reduction (3M). |
|
|
This is the default 32-bit integer mode and uses compute and intermediate storage precisions of at least 32-bits. |
|
|
Uses 32-bit integer arithmetic for all phases of calculations. |
|
Note
Setting the environment variable NVIDIA_TF32_OVERRIDE = 0 will override any defaults or programmatic configuration of NVIDIA libraries, and consequently, cuBLAS will not accelerate single-precision computations with TF32 tensor cores.
2.2.12. cublasEmulationStrategy_t
cublasEmulationStrategy_t enumerate type is used in cublasSetEmulationStrategy() to choose how to leverage floating point emulation algorithms.
Value |
Meaning |
|---|---|
|
This is the default emulation strategy and is equivalent to |
|
A strategy which utilizes emulation whenever it provides a performance benefit. |
|
A strategy which utilizes emulation whenever possible. |
Note
In general, the cublasSetEmulationStrategy() function takes precedence over the environment variable setting.
However, setting the environment variable CUBLAS_EMULATION_STRATEGY to performant or eager will override the default emulation strategy with the corresponding emulation strategy, even if the default strategy was set by the function call.
2.3. CUDA Datatypes Reference
The chapter describes types shared by multiple CUDA Libraries and defined in the header file library_types.h.
2.3.1. cudaDataType_t
The cudaDataType_t type is an enumerant to specify the data precision. It is used when the data reference does not carry the type itself (e.g void *)
For example, it is used in the routine cublasSgemmEx().
Value |
Meaning |
|---|---|
|
The data type is a 16-bit real half precision floating-point |
|
The data type is a 32-bit structure comprised of two half precision floating-points representing a complex number. |
|
The data type is a 16-bit real bfloat16 floating-point |
|
The data type is a 32-bit structure comprised of two bfloat16 floating-points representing a complex number. |
|
The data type is a 32-bit real single precision floating-point |
|
The data type is a 64-bit structure comprised of two single precision floating-points representing a complex number. |
|
The data type is a 64-bit real double precision floating-point |
|
The data type is a 128-bit structure comprised of two double precision floating-points representing a complex number. |
|
The data type is a 8-bit real signed integer |
|
The data type is a 16-bit structure comprised of two 8-bit signed integers representing a complex number. |
|
The data type is a 8-bit real unsigned integer |
|
The data type is a 16-bit structure comprised of two 8-bit unsigned integers representing a complex number. |
|
The data type is a 32-bit real signed integer |
|
The data type is a 64-bit structure comprised of two 32-bit signed integers representing a complex number. |
|
The data type is an 8-bit real floating point in E4M3 format |
|
The data type is an 8-bit real floating point in E5M2 format |
|
The data type is a 4-bit real floating point in E2M1 format |
2.3.2. cudaEmulationStrategy_t
The cudaEmulationStrategy_t is a parameter to specify how to leverage floating point emulation algorithms. This is equivalent to cublasEmulationStrategy_t.
2.3.3. cudaEmulationMantissaControl_t
The cudaEmulationMantissaControl_t is an enumerated type to specify how to configure how the number of mantissa bits are calculated in floating point emulation algorithms.
See See cublasSetFixedPointEmulationMantissaControl() and cublasGetFixedPointEmulationMaxMantissaBitCount().
Value |
Meaning |
|---|---|
|
The number of retained mantissa bits is computed at runtime to ensure the same or better accuracy than the native floating point representation. |
|
The number of retained mantissa bits is fixed at runtime. |
2.3.4. cudaEmulationSpecialValuesSupport_t
The cudaEmulationSpecialValuesSupport_t is an enumerated type to specify how to configure which floating point special values are required to be supported by
floating point emulation algorithms. See cublasSetEmulationSpecialValuesSupport() and cublasGetEmulationSpecialValuesSupport().
Value |
Meaning |
|---|---|
|
The default special value support mask which contains support for signed infinities and NaN values. |
|
There are no requirements for emulation algorithms to support special values. |
|
Require emulation algorithms to handle signed infinity inputs and outputs. |
|
Require emulation algorithms to handle NaN inputs and outputs. |
2.3.5. libraryPropertyType_t
The libraryPropertyType_t is used as a parameter to specify which property is requested when using the routine cublasGetProperty()
Value |
Meaning |
|---|---|
|
enumerant to query the major version |
|
enumerant to query the minor version |
|
number to identify the patch level |
2.4. cuBLAS Helper Function Reference
2.4.1. cublasCreate()
cublasStatus_t
cublasCreate(cublasHandle_t *handle)
This function initializes the cuBLAS library and creates a handle to an opaque structure holding the cuBLAS library context. It allocates hardware resources on the host and device and must be called prior to making any other cuBLAS library calls.
The cuBLAS library context is tied to the current CUDA device. To use the library on multiple devices, one cuBLAS handle needs to be created for each device. See also cuBLAS Context.
For a given device, multiple cuBLAS handles with different configurations can be created. For multi-threaded applications that use the same device from different threads, the recommended programming model is to create one cuBLAS handle per thread and use that cuBLAS handle for the entire life of the thread.
Because cublasCreate() allocates some internal resources and the release of those resources by calling cublasDestroy() will implicitly call cudaDeviceSynchronize(), it is recommended to minimize the number of times these functions are called.
Return Value |
Meaning |
|---|---|
|
The initialization succeeded |
|
The CUDA™ Runtime initialization failed |
|
The resources could not be allocated |
|
|
2.4.2. cublasDestroy()
cublasStatus_t
cublasDestroy(cublasHandle_t handle)
This function releases hardware resources used by the cuBLAS library. This function is usually the last call with a particular handle to the cuBLAS library. Because cublasCreate() allocates some internal resources and the release of those resources by calling cublasDestroy() will implicitly call cudaDeviceSynchronize(), it is recommended to minimize the number of times these functions are called.
Return Value |
Meaning |
|---|---|
|
the shut down succeeded |
|
the library was not initialized |
2.4.3. cublasGetVersion()
cublasStatus_t
cublasGetVersion(cublasHandle_t handle, int *version)
This function returns the version number of the cuBLAS library.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
|
Note
This function can be safely called with handle set to NULL. This allows users to get the version of the library without a handle. Another way to do this is with cublasGetProperty().
2.4.4. cublasGetProperty()
cublasStatus_t
cublasGetProperty(libraryPropertyType type, int *value)
This function returns the value of the requested property in memory pointed to by value. Refer to libraryPropertyType for supported types.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
Invalid type or value
|
2.4.5. cublasGetStatusName()
const char* cublasGetStatusName(cublasStatus_t status)
This function returns the string representation of a given status.
Return Value |
Meaning |
|---|---|
NULL-terminated string |
The string representation of the |
2.4.6. cublasGetStatusString()
const char* cublasGetStatusString(cublasStatus_t status)
This function returns the description string for a given status.
Return Value |
Meaning |
|---|---|
NULL-terminated string |
The description of the |
2.4.7. cublasSetStream()
cublasStatus_t
cublasSetStream(cublasHandle_t handle, cudaStream_t streamId)
This function sets the cuBLAS library stream, which will be used to execute all subsequent calls to the cuBLAS library functions. If the cuBLAS library stream is not set, all kernels use the default NULL stream. In particular, this routine can be used to change the stream between kernel launches and then to reset the cuBLAS library stream back to NULL. Additionally this function unconditionally resets the cuBLAS library workspace back to the default workspace pool (see cublasSetWorkspace()).
Return Value |
Meaning |
|---|---|
|
the stream was set successfully |
|
the library was not initialized |
2.4.8. cublasSetWorkspace()
cublasStatus_t
cublasSetWorkspace(cublasHandle_t handle, void *workspace, size_t workspaceSizeInBytes)
This function sets the cuBLAS library workspace to a user-owned device buffer, which will be used to execute all subsequent calls to the cuBLAS library functions (on the currently set stream). If the cuBLAS library workspace is not set, all kernels will use the default workspace pool allocated during the cuBLAS context creation. In particular, this routine can be used to change the workspace between kernel launches. The workspace pointer has to be aligned to at least 256 bytes, otherwise CUBLAS_STATUS_INVALID_VALUE error is returned. The cublasSetStream() function unconditionally resets the cuBLAS library workspace back to the default workspace pool. Calling this function, including with workspaceSizeInBytes equal to 0, will prevent the cuBLAS library from utilizing the default workspace. Too small value of workspaceSizeInBytes may cause some routines to fail with CUBLAS_STATUS_ALLOC_FAILED error returned or cause large regressions in performance. Workspace size equal to or larger than 16KiB is enough to prevent CUBLAS_STATUS_ALLOC_FAILED error, while a larger workspace can provide performance benefits for some routines.
Note
If the stream set by cublasSetStream() is cudaStreamPerThread and there are multiple threads using the same cuBLAS library handle, then users must manually manage synchronization to avoid possible race conditions in the user provided workspace. Alternatively, users may rely on the default workspace pool which safely guards against race conditions.
Warning
cuBLAS functions may invoke more than one CUDA kernel, and rely on workspace being intact between the invocations. Hence, if cuBLAS handle is configured with user-provided workspace and is being used from multiple threads, it is user’s responsibility to serialize cuBLAS calls between threads, as otherwise the kernels from different cuBLAS invocations might interleave and invalidate the assumptions each of them makes regarding workspace intactness. The default workspace pool managed by cuBLAS is thread safe.
The table below shows the recommended size of user-provided workspace. This is based on the cuBLAS default workspace pool size which is GPU architecture dependent.
GPU Architecture |
Recommended workspace size |
|---|---|
NVIDIA Hopper Architecture (sm90) |
32 MiB |
NVIDIA Blackwell Architecture (sm10x) |
32 MiB |
NVIDIA Blackwell Architecture (sm12x) |
32 MiB |
Other |
4 MiB |
Note
If the cuBLAS library is configured to utilize fixed-point emulation, which can be done by setting the corresponding math mode in cublasSetMathMode() or calling APIs with CUBLAS_COMPUTE_64F_EMULATED_FIXEDPOINT, it can be beneficial to provide more workspace than recommended for the GPU architecture. See Fixed-Point Workspace Requirements for more details.
The possible error values returned by this function and their meanings are listed below.
Return Value |
Meaning |
|---|---|
|
The stream was set successfully |
|
The library was not initialized |
|
The |
2.4.9. cublasGetStream()
cublasStatus_t
cublasGetStream(cublasHandle_t handle, cudaStream_t *streamId)
This function gets the cuBLAS library stream, which is being used to execute all calls to the cuBLAS library functions. If the cuBLAS library stream is not set, all kernels use the default NULL stream.
Return Value |
Meaning |
|---|---|
|
the stream was returned successfully |
|
the library was not initialized |
|
|
2.4.10. cublasGetPointerMode()
cublasStatus_t
cublasGetPointerMode(cublasHandle_t handle, cublasPointerMode_t *mode)
This function obtains the pointer mode used by the cuBLAS library. Please see the section on the cublasPointerMode_t type for more details.
Return Value |
Meaning |
|---|---|
|
The pointer mode was obtained successfully |
|
The library was not initialized |
|
|
2.4.11. cublasSetPointerMode()
cublasStatus_t
cublasSetPointerMode(cublasHandle_t handle, cublasPointerMode_t mode)
This function sets the pointer mode used by the cuBLAS library. The default is for the values to be passed by reference on the host. Please see the section on the cublasPointerMode_t type for more details.
Return Value |
Meaning |
|---|---|
|
The pointer mode was set successfully |
|
The library was not initialized |
|
|
2.4.12. cublasSetVector()
cublasStatus_t
cublasSetVector(int n, int elemSize,
const void *x, int incx, void *y, int incy)
This function supports the 64-bit Integer Interface.
This function copies n elements from a vector x in host memory space to a vector y in GPU memory space. Elements in both vectors are assumed to have a size of elemSize bytes. The storage spacing between consecutive elements is given by incx for the source vector x and by incy for the destination vector y.
Since column-major format for two-dimensional matrices is assumed, if a vector is part of a matrix, a vector increment equal to 1 accesses a (partial) column of that matrix. Similarly, using an increment equal to the leading dimension of the matrix results in accesses to a (partial) row of that matrix.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.13. cublasGetVector()
cublasStatus_t
cublasGetVector(int n, int elemSize,
const void *x, int incx, void *y, int incy)
This function supports the 64-bit Integer Interface.
This function copies n elements from a vector x in GPU memory space to a vector y in host memory space. Elements in both vectors are assumed to have a size of elemSize bytes. The storage spacing between consecutive elements is given by incx for the source vector and incy for the destination vector y.
Since column-major format for two-dimensional matrices is assumed, if a vector is part of a matrix, a vector increment equal to 1 accesses a (partial) column of that matrix. Similarly, using an increment equal to the leading dimension of the matrix results in accesses to a (partial) row of that matrix.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.14. cublasSetMatrix()
cublasStatus_t
cublasSetMatrix(int rows, int cols, int elemSize,
const void *A, int lda, void *B, int ldb)
This function supports the 64-bit Integer Interface.
This function copies a tile of rows x cols elements from a matrix A in host memory space to a matrix B in GPU memory space. It is assumed that each element requires storage of elemSize bytes and that both matrices are stored in column-major format, with the leading dimension of the source matrix A and destination matrix B given in lda and ldb, respectively. The leading dimension indicates the number of rows of the allocated matrix, even if only a submatrix of it is being used.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.15. cublasGetMatrix()
cublasStatus_t
cublasGetMatrix(int rows, int cols, int elemSize,
const void *A, int lda, void *B, int ldb)
This function supports the 64-bit Integer Interface.
This function copies a tile of rows x cols elements from a matrix A in GPU memory space to a matrix B in host memory space. It is assumed that each element requires storage of elemSize bytes and that both matrices are stored in column-major format, with the leading dimension of the source matrix A and destination matrix B given in lda and ldb, respectively. The leading dimension indicates the number of rows of the allocated matrix, even if only a submatrix of it is being used.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.16. cublasSetVectorAsync()
cublasStatus_t
cublasSetVectorAsync(int n, int elemSize, const void *hostPtr, int incx,
void *devicePtr, int incy, cudaStream_t stream)
This function supports the 64-bit Integer Interface.
This function has the same functionality as cublasSetVector(), with the exception that the data transfer is done asynchronously (with respect to the host) using the given CUDA™ stream parameter.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.17. cublasGetVectorAsync()
cublasStatus_t
cublasGetVectorAsync(int n, int elemSize, const void *devicePtr, int incx,
void *hostPtr, int incy, cudaStream_t stream)
This function supports the 64-bit Integer Interface.
This function has the same functionality as cublasGetVector(), with the exception that the data transfer is done asynchronously (with respect to the host) using the given CUDA™ stream parameter.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.18. cublasSetMatrixAsync()
cublasStatus_t
cublasSetMatrixAsync(int rows, int cols, int elemSize, const void *A,
int lda, void *B, int ldb, cudaStream_t stream)
This function supports the 64-bit Integer Interface.
This function has the same functionality as cublasSetMatrix(), with the exception that the data transfer is done asynchronously (with respect to the host) using the given CUDA™ stream parameter.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.19. cublasGetMatrixAsync()
cublasStatus_t
cublasGetMatrixAsync(int rows, int cols, int elemSize, const void *A,
int lda, void *B, int ldb, cudaStream_t stream)
This function supports the 64-bit Integer Interface.
This function has the same functionality as cublasGetMatrix(), with the exception that the data transfer is done asynchronously (with respect to the host) using the given CUDA™ stream parameter.
Return Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The parameters |
|
There was an error accessing GPU memory |
2.4.20. cublasSetAtomicsMode()
cublasStatus_t cublasSetAtomicsMode(cublasHandlet handle, cublasAtomicsMode_t mode)
Some routines like cublas<t>symv() and cublas<t>hemv() have an alternate implementation that use atomics to cumulate results. This implementation is generally significantly faster but can generate results that are not strictly identical from one run to the others. Mathematically, those different results are not significant but when debugging those differences can be prejudicial.
This function allows or disallows the usage of atomics in the cuBLAS library for all routines which have an alternate implementation. When not explicitly specified in the documentation of any cuBLAS routine, it means that this routine does not have an alternate implementation that use atomics. When atomics mode is disabled, each cuBLAS routine should produce the same results from one run to the other when called with identical parameters on the same Hardware.
The default atomics mode of default initialized cublasHandle_t object is CUBLAS_ATOMICS_NOT_ALLOWED. Please see the section on the type for more details.
Return Value |
Meaning |
|---|---|
|
the atomics mode was set successfully |
|
the library was not initialized |
2.4.21. cublasGetAtomicsMode()
cublasStatus_t cublasGetAtomicsMode(cublasHandle_t handle, cublasAtomicsMode_t *mode)
This function queries the atomic mode of a specific cuBLAS context.
The default atomics mode of default initialized cublasHandle_t object is CUBLAS_ATOMICS_NOT_ALLOWED. Please see the section on the type for more details.
Return Value |
Meaning |
|---|---|
|
The atomics mode was queried successfully |
|
The library was not initialized |
|
The argument |
2.4.22. cublasSetMathMode()
cublasStatus_t cublasSetMathMode(cublasHandle_t handle, cublasMath_t mode)
The cublasSetMathMode() function enables you to choose the compute precision modes as defined by cublasMath_t. Users are allowed to set the compute precision mode as a logical combination of them (except the deprecated CUBLAS_TENSOR_OP_MATH). For example, cublasSetMathMode(handle, CUBLAS_DEFAULT_MATH | CUBLAS_MATH_DISALLOW_REDUCED_PRECISION_REDUCTION). Please note that the default math mode is CUBLAS_DEFAULT_MATH.
For matrix and compute precisions allowed for cublasGemmEx() and cublasLtMatmul() APIs and their strided variants please refer to: cublasGemmEx() , cublasGemmBatchedEx(), cublasGemmStridedBatchedEx(), and cublasLtMatmul().
Return Value |
Meaning |
|---|---|
|
The math mode was set successfully. |
|
An invalid value for mode was specified. |
|
The library was not initialized. |
2.4.23. cublasGetMathMode()
cublasStatus_t cublasGetMathMode(cublasHandle_t handle, cublasMath_t *mode)
This function returns the math mode used by the library routines.
Return Value |
Meaning |
|---|---|
|
The math type was returned successfully. |
|
If |
|
The library was not initialized. |
2.4.24. cublasSetSmCountTarget()
cublasStatus_t cublasSetSmCountTarget(cublasHandle_t handle, int smCountTarget)
The cublasSetSmCountTarget() function allows overriding the number of multiprocessors available to the library during kernels execution.
This option can be used to improve the library performance when cuBLAS routines are known to run concurrently with other work on different CUDA streams. For example, on an NVIDIA A100 GPU, which has 108 multiprocessors, when there is a concurrent kenrel running with grid size of 8, one can use cublasSetSmCountTarget() with smCountTarget set to 100 to override the library heuristics to optimize for running on the remaining 100 multiprocessors.
When set to 0, the library returns to its default behavior. The input value should not exceed the device’s multiprocessor count, which can be obtained using cudaDeviceGetAttribute. Negative values are not accepted.
The user must ensure thread safety when modifying the library handle with this routine similar to when using cublasSetStream(), etc.
Return Value |
Meaning |
|---|---|
|
SM count target was set successfully. |
|
The value of |
|
The library was not initialized. |
2.4.25. cublasGetSmCountTarget()
cublasStatus_t cublasGetSmCountTarget(cublasHandle_t handle, int *smCountTarget)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
SM count target was returned successfully. |
|
smCountTarget is NULL. |
|
the library was not initialized. |
2.4.26. cublasSetEmulationStrategy()
cublasStatus_t cublasSetEmulationStrategy(cublasHandle_t handle, cublasEmulationStrategy_t emulationStrategy)
The cublasSetEmulationStrategy() function enables you to select how the library should make use of floating point emulation. For more details, please see cublasEmulationStrategy_t.
Return Value |
Meaning |
|---|---|
|
The emulation strategy was set successfully. |
|
An invalid value for emulation strategy was specified. |
|
The library was not initialized. |
2.4.27. cublasGetEmulationStrategy()
cublasStatus_t cublasGetEmulationStrategy(cublasHandle_t handle, cublasEmulationStrategy_t *emulationStrategy)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
emulation strategy was returned successfully. |
|
emulationStrategy is NULL. |
|
the library was not initialized. |
2.4.28. cublasGetEmulationSpecialValuesSupport()
cublasStatus_t cublasGetEmulationSpecialValuesSupport(cublasHandle_t handle, cudaEmulationSpecialValuesSupport *mask)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
emulation special values support was returned successfully. |
|
mask is NULL. |
|
the library was not initialized. |
2.4.29. cublasSetEmulationSpecialValuesSupport()
cublasStatus_t cublasSetEmulationSpecialValuesSupport(cublasHandle_t handle, cudaEmulationSpecialValuesSupport mask)
This function sets the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
emulation special values support was set successfully. |
|
mask is outside of the allowed range. |
|
the library was not initialized. |
2.4.30. cublasGetFixedPointEmulationMantissaControl()
cublasStatus_t cublasGetFixedPointEmulationMantissaControl(cublasHandle_t handle, cudaEmulationMantissaControl *mantissaControl)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
fixed-point emulation mantissa control was returned successfully. |
|
mantissaControl is NULL. |
|
the library was not initialized. |
2.4.31. cublasSetFixedPointEmulationMantissaControl()
cublasStatus_t cublasSetFixedPointEmulationMantissaControl(cublasHandle_t handle, cudaEmulationMantissaControl mantissaControl)
This function sets the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
fixed-point emulation mantissa control was set successfully. |
|
mantissaControl is outside of the allowed range. |
|
the library was not initialized. |
2.4.32. cublasGetFixedPointEmulationMaxMantissaBitCount()
cublasStatus_t cublasGetFixedPointEmulationMaxMantissaBitCount(cublasHandle_t handle, int *maxMantissaBitCount)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
maxMantissaBitCount was returned successfully. |
|
maxMantissaBitCount is NULL. |
|
the library was not initialized. |
2.4.33. cublasSetFixedPointEmulationMaxMantissaBitCount()
cublasStatus_t cublasSetFixedPointEmulationMaxMantissaBitCount(cublasHandle_t handle, int maxMantissaBitCount)
This function sets the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
maxMantissaBitCount was set successfully. |
|
maxMantissaBitCount is outside of the allowed range. |
|
the library was not initialized. |
2.4.34. cublasGetFixedPointEmulationMantissaBitOffset()
cublasStatus_t cublasGetFixedPointEmulationMantissaBitOffset(cublasHandle_t handle, int *mantissaBitOffset)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
mantissaBitOffset was returned successfully. |
|
mantissaBitOffset is NULL. |
|
the library was not initialized. |
2.4.35. cublasSetFixedPointEmulationMantissaBitOffset()
cublasStatus_t cublasSetFixedPointEmulationMantissaBitOffset(cublasHandle_t handle, int mantissaBitOffset)
This function sets the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
mantissaBitOffset was set successfully. |
|
mantissaBitOffset is outside of the allowed range. |
|
the library was not initialized. |
2.4.36. cublasGetFixedPointEmulationMantissaBitCountPointer()
cublasStatus_t cublasGetFixedPointEmulationMantissaBitCountPointer(cublasHandle_t handle, int **mantissaBitCount)
This function obtains the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
mantissaBitCount was returned successfully. |
|
mantissaBitCount is NULL. |
|
the library was not initialized. |
2.4.37. cublasSetFixedPointEmulationMantissaBitCountPointer()
cublasStatus_t cublasSetFixedPointEmulationMantissaBitCountPointer(cublasHandle_t handle, int *mantissaBitCount)
This function sets the value previously programmed to the library handle.
Return Value |
Meaning |
|---|---|
|
mantissaBitCount was set successfully. |
|
mantissaBitCount is outside of the allowed range. |
|
the library was not initialized. |
2.4.38. cublasLoggerConfigure()
cublasStatus_t cublasLoggerConfigure(
int logIsOn,
int logToStdOut,
int logToStdErr,
const char* logFileName)
This function configures logging during runtime. Besides this type of configuration, it is possible to configure logging with special environment variables which will be checked by libcublas:
CUBLAS_LOGINFO_DBG- setting this environment variable to1means turning logging on (by default logging is off).CUBLAS_LOGDEST_DBG- this environment variable encodes where to write the log to:stdout,stderrmean to write log messages to standard output or error streams, respectively. Other values are interpreted as file names.
Parameters
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
logIsOn |
host |
input |
Turn on/off logging completely. By default is off, but is turned on by calling cublasSetLoggerCallback() to user defined callback function. |
logToStdOut |
host |
input |
Turn on/off logging to standard output I/O stream. By default is off. |
logToStdErr |
host |
input |
Turn on/off logging to standard error I/O stream. By default is off. |
logFileName |
host |
input |
Turn on/off logging to file in filesystem specified by it’s name. cublasLoggerConfigure() copies the content of |
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
2.4.39. cublasGetLoggerCallback()
cublasStatus_t cublasGetLoggerCallback(
cublasLogCallback* userCallback)
This function retrieves function pointer to previously installed custom user defined callback function via cublasSetLoggerCallback() or zero otherwise.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
userCallback |
host |
output |
Pointer to user defined callback function. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
|
2.4.40. cublasSetLoggerCallback()
cublasStatus_t cublasSetLoggerCallback(
cublasLogCallback userCallback)
This function installs a custom user defined callback function via cublas C public API.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
userCallback |
host |
input |
Pointer to user defined callback function. |
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
2.5. cuBLAS Level-1 Function Reference
In this chapter we describe the Level-1 Basic Linear Algebra Subprograms (BLAS1) functions that perform scalar and vector based operations. We will use abbreviations <type> for type and <t> for the corresponding short type to make a more concise and clear presentation of the implemented functions. Unless otherwise specified <type> and <t> have the following meanings:
<type> |
<t> |
Meaning |
|---|---|---|
|
|
real single-precision |
|
|
real double-precision |
|
|
complex single-precision |
|
|
complex double-precision |
When the parameters and returned values of the function differ, which sometimes happens for complex input, the <t> can also be Sc, Cs, Dz and Zd.
The abbreviation \(\mathbf{Re}(\cdot)\) and \(\mathbf{Im}(\cdot)\) will stand for the real and imaginary part of a number, respectively. Since imaginary part of a real number does not exist, we will consider it to be zero and can usually simply discard it from the equation where it is being used. Also, the \(\bar{\alpha}\) will denote the complex conjugate of \(\alpha\) .
In general throughout the documentation, the lower case Greek symbols \(\alpha\) and \(\beta\) will denote scalars, lower case English letters in bold type \(\mathbf{x}\) and \(\mathbf{y}\) will denote vectors and capital English letters \(A\) , \(B\) and \(C\) will denote matrices.
2.5.1. cublasI<t>amax()
cublasStatus_t cublasIsamax(cublasHandle_t handle, int n,
const float *x, int incx, int *result)
cublasStatus_t cublasIdamax(cublasHandle_t handle, int n,
const double *x, int incx, int *result)
cublasStatus_t cublasIcamax(cublasHandle_t handle, int n,
const cuComplex *x, int incx, int *result)
cublasStatus_t cublasIzamax(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx, int *result)
This function supports the 64-bit Integer Interface.
This function finds the (smallest) index of the element of the maximum magnitude. Hence, the result is the first \(i\) such that \(\left| \mathbf{Im}\left( {x\lbrack j\rbrack} \right) \middle| + \middle| \mathbf{Re}\left( {x\lbrack j\rbrack} \right) \right|\) is maximum for \(i = 1,\ldots,n\) and \(j = 1 + \left( {i - 1} \right)*\text{ incx}\) . Notice that the last equation reflects 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with elements. |
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting index, which is set to |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
2.5.2. cublasI<t>amin()
cublasStatus_t cublasIsamin(cublasHandle_t handle, int n,
const float *x, int incx, int *result)
cublasStatus_t cublasIdamin(cublasHandle_t handle, int n,
const double *x, int incx, int *result)
cublasStatus_t cublasIcamin(cublasHandle_t handle, int n,
const cuComplex *x, int incx, int *result)
cublasStatus_t cublasIzamin(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx, int *result)
This function supports the 64-bit Integer Interface.
This function finds the (smallest) index of the element of the minimum magnitude. Hence, the result is the first \(i\) such that \(\left| \mathbf{Im}\left( {x\lbrack j\rbrack} \right) \middle| + \middle| \mathbf{Re}\left( {x\lbrack j\rbrack} \right) \right|\) is minimum for \(i = 1,\ldots,n\) and \(j = 1 + \left( {i - 1} \right)*\text{incx}\) Notice that the last equation reflects 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with elements. |
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting index, which is set to |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
2.5.3. cublas<t>asum()
cublasStatus_t cublasSasum(cublasHandle_t handle, int n,
const float *x, int incx, float *result)
cublasStatus_t cublasDasum(cublasHandle_t handle, int n,
const double *x, int incx, double *result)
cublasStatus_t cublasScasum(cublasHandle_t handle, int n,
const cuComplex *x, int incx, float *result)
cublasStatus_t cublasDzasum(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx, double *result)
This function supports the 64-bit Integer Interface.
This function computes the sum of the absolute values of the elements of vector x. Hence, the result is \(\left. \sum_{i = 1}^{n} \middle| \mathbf{Im}\left( {x\lbrack j\rbrack} \right) \middle| + \middle| \mathbf{Re}\left( {x\lbrack j\rbrack} \right) \right|\) where \(j = 1 + \left( {i - 1} \right)*\text{incx}\) . Notice that the last equation reflects 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with elements. |
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting sum, which is set to |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
2.5.4. cublas<t>axpy()
cublasStatus_t cublasSaxpy(cublasHandle_t handle, int n,
const float *alpha,
const float *x, int incx,
float *y, int incy)
cublasStatus_t cublasDaxpy(cublasHandle_t handle, int n,
const double *alpha,
const double *x, int incx,
double *y, int incy)
cublasStatus_t cublasCaxpy(cublasHandle_t handle, int n,
const cuComplex *alpha,
const cuComplex *x, int incx,
cuComplex *y, int incy)
cublasStatus_t cublasZaxpy(cublasHandle_t handle, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function multiplies the vector x by the scalar \(\alpha\) and adds it to the vector y overwriting the latest vector with the result. Hence, the performed operation is \(\mathbf{y}\lbrack j\rbrack = \alpha \times \mathbf{x}\lbrack k\rbrack + \mathbf{y}\lbrack j\rbrack\) for \(i = 1,\ldots,n\) , \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.5. cublas<t>copy()
cublasStatus_t cublasScopy(cublasHandle_t handle, int n,
const float *x, int incx,
float *y, int incy)
cublasStatus_t cublasDcopy(cublasHandle_t handle, int n,
const double *x, int incx,
double *y, int incy)
cublasStatus_t cublasCcopy(cublasHandle_t handle, int n,
const cuComplex *x, int incx,
cuComplex *y, int incy)
cublasStatus_t cublasZcopy(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function copies the vector x into the vector y. Hence, the performed operation is \(\mathbf{y}\lbrack j\rbrack = \mathbf{x}\lbrack k\rbrack\) for \(i = 1,\ldots,n\) , \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.6. cublas<t>dot()
cublasStatus_t cublasSdot (cublasHandle_t handle, int n,
const float *x, int incx,
const float *y, int incy,
float *result)
cublasStatus_t cublasDdot (cublasHandle_t handle, int n,
const double *x, int incx,
const double *y, int incy,
double *result)
cublasStatus_t cublasCdotu(cublasHandle_t handle, int n,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *result)
cublasStatus_t cublasCdotc(cublasHandle_t handle, int n,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *result)
cublasStatus_t cublasZdotu(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *result)
cublasStatus_t cublasZdotc(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *result)
This function supports the 64-bit Integer Interface.
This function computes the dot product of vectors x and y. Hence, the result is \(\sum_{i = 1}^{n}\left( {\mathbf{x}\lbrack k\rbrack \times \mathbf{y}\lbrack j\rbrack} \right)\) where \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that in the first equation the conjugate of the element of vector x should be used if the function name ends in character ‘c’ and that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting dot product, which is set to |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.7. cublas<t>nrm2()
cublasStatus_t cublasSnrm2(cublasHandle_t handle, int n,
const float *x, int incx, float *result)
cublasStatus_t cublasDnrm2(cublasHandle_t handle, int n,
const double *x, int incx, double *result)
cublasStatus_t cublasScnrm2(cublasHandle_t handle, int n,
const cuComplex *x, int incx, float *result)
cublasStatus_t cublasDznrm2(cublasHandle_t handle, int n,
const cuDoubleComplex *x, int incx, double *result)
This function supports the 64-bit Integer Interface.
This function computes the Euclidean norm of the vector x. The code uses a multiphase model of accumulation to avoid intermediate underflow and overflow, with the result being equivalent to \(\sqrt{\sum_{i = 1}^{n}\left( {\mathbf{x}\lbrack j\rbrack \times \mathbf{x}\lbrack j\rbrack} \right)}\) where \(j = 1 + \left( {i - 1} \right)*\text{incx}\) in exact arithmetic. Notice that the last equation reflects 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting norm, which is set to |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
2.5.8. cublas<t>rot()
cublasStatus_t cublasSrot(cublasHandle_t handle, int n,
float *x, int incx,
float *y, int incy,
const float *c, const float *s)
cublasStatus_t cublasDrot(cublasHandle_t handle, int n,
double *x, int incx,
double *y, int incy,
const double *c, const double *s)
cublasStatus_t cublasCrot(cublasHandle_t handle, int n,
cuComplex *x, int incx,
cuComplex *y, int incy,
const float *c, const cuComplex *s)
cublasStatus_t cublasCsrot(cublasHandle_t handle, int n,
cuComplex *x, int incx,
cuComplex *y, int incy,
const float *c, const float *s)
cublasStatus_t cublasZrot(cublasHandle_t handle, int n,
cuDoubleComplex *x, int incx,
cuDoubleComplex *y, int incy,
const double *c, const cuDoubleComplex *s)
cublasStatus_t cublasZdrot(cublasHandle_t handle, int n,
cuDoubleComplex *x, int incx,
cuDoubleComplex *y, int incy,
const double *c, const double *s)
This function supports the 64-bit Integer Interface.
This function applies Givens rotation matrix (i.e., rotation in the x,y plane counter-clockwise by angle defined by \(cos(alpha) = c\), \(sin(alpha) = s\)):
\(G = \begin{pmatrix} c & s \\ {- s} & c \\ \end{pmatrix}\)
to vectors x and y.
Hence, the result is \(\mathbf{x}\lbrack k\rbrack = c \times \mathbf{x}\lbrack k\rbrack + s \times \mathbf{y}\lbrack j\rbrack\) and \(\mathbf{y}\lbrack j\rbrack = - s \times \mathbf{x}\lbrack k\rbrack + c \times \mathbf{y}\lbrack j\rbrack\) where \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
Cosine element of the rotation matrix. |
|
host or device |
input |
Sine element of the rotation matrix. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.9. cublas<t>rotg()
cublasStatus_t cublasSrotg(cublasHandle_t handle,
float *a, float *b,
float *c, float *s)
cublasStatus_t cublasDrotg(cublasHandle_t handle,
double *a, double *b,
double *c, double *s)
cublasStatus_t cublasCrotg(cublasHandle_t handle,
cuComplex *a, cuComplex *b,
float *c, cuComplex *s)
cublasStatus_t cublasZrotg(cublasHandle_t handle,
cuDoubleComplex *a, cuDoubleComplex *b,
double *c, cuDoubleComplex *s)
This function supports the 64-bit Integer Interface.
This function constructs the Givens rotation matrix
\(G = \begin{pmatrix} c & s \\ {- s} & c \\ \end{pmatrix}\)
that zeros out the second entry of a \(2 \times 1\) vector \(\left( {a,b} \right)^{T}\) .
Then, for real numbers we can write
\(\begin{pmatrix} c & s \\ {- s} & c \\ \end{pmatrix}\begin{pmatrix} a \\ b \\ \end{pmatrix} = \begin{pmatrix} r \\ 0 \\ \end{pmatrix}\)
where \(c^{2} + s^{2} = 1\) and \(r = \pm \sqrt{a^{2} + b^{2}}\) . The parameters \(a\) and \(b\) are overwritten with \(r\) and \(z\) , respectively. The value of \(z\) is such that \(c\) and \(s\) may be recovered using the following rules:
\(\left( {c,s} \right) = \begin{cases} \left( {\sqrt{1 - z^{2}},z} \right) & {\text{ if }\left| z \middle| < 1 \right.} \\ \left( {0.0,1.0} \right) & {\text{ if }\left| z \middle| = 1 \right.} \\ \left( 1/z,\sqrt{1 - z^{2}} \right) & {\text{ if }\left| z \middle| > 1 \right.} \\ \end{cases}\)
For complex numbers we can write
\(\begin{pmatrix} c & s \\ {- \bar{s}} & c \\ \end{pmatrix}\begin{pmatrix} a \\ b \\ \end{pmatrix} = \begin{pmatrix} r \\ 0 \\ \end{pmatrix}\)
where \(c^{2} + \left( {\bar{s} \times s} \right) = 1\) and \(r = \frac{a}{|a|} \times \parallel \left( {a,b} \right)^{T} \parallel_{2}\) with \(\parallel \left( {a,b} \right)^{T} \parallel_{2} = \sqrt{\left| a|^{2} + \middle| B|^{2} \right.}\) for \(a \neq 0\) and \(r = b\) for \(a = 0\) . Finally, the parameter \(a\) is overwritten with \(r\) on exit.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
host or device |
in/out |
<type> scalar that is overwritten with \(r\) . |
|
host or device |
in/out |
<type> scalar that is overwritten with \(z\) . |
|
host or device |
output |
Cosine element of the rotation matrix. |
|
host or device |
output |
Sine element of the rotation matrix. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.10. cublas<t>rotm()
cublasStatus_t cublasSrotm(cublasHandle_t handle, int n, float *x, int incx,
float *y, int incy, const float* param)
cublasStatus_t cublasDrotm(cublasHandle_t handle, int n, double *x, int incx,
double *y, int incy, const double* param)
This function supports the 64-bit Integer Interface.
This function applies the modified Givens transformation
\(H = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \\ \end{pmatrix}\)
to vectors x and y.
Hence, the result is \(\mathbf{x}\lbrack k\rbrack = h_{11} \times \mathbf{x}\lbrack k\rbrack + h_{12} \times \mathbf{y}\lbrack j\rbrack\) and \(\mathbf{y}\lbrack j\rbrack = h_{21} \times \mathbf{x}\lbrack k\rbrack + h_{22} \times \mathbf{y}\lbrack j\rbrack\) where \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
The elements , , and of matrix \(H\) are stored in param[1], param[2], param[3] and param[4], respectively. The flag = param[0] defines the following predefined values for the matrix \(H\) entries
|
|
|
|
|---|---|---|---|
\(\begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \\ \end{pmatrix}\) |
\(\begin{pmatrix} {1.0} & h_{12} \\ h_{21} & {1.0} \\ \end{pmatrix}\) |
\(\begin{pmatrix} h_{11} & {1.0} \\ {- 1.0} & h_{22} \\ \end{pmatrix}\) |
\(\begin{pmatrix} {1.0} & {0.0} \\ {0.0} & {1.0} \\ \end{pmatrix}\) |
Notice that the values -1.0, 0.0 and 1.0 implied by the flag are not stored in param.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> vector of 5 elements, where |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.11. cublas<t>rotmg()
cublasStatus_t cublasSrotmg(cublasHandle_t handle, float *d1, float *d2,
float *x1, const float *y1, float *param)
cublasStatus_t cublasDrotmg(cublasHandle_t handle, double *d1, double *d2,
double *x1, const double *y1, double *param)
This function supports the 64-bit Integer Interface.
This function constructs the modified Givens transformation
\(H = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \\ \end{pmatrix}\)
that zeros out the second entry of a \(2 \times 1\) vector \(\left( {\sqrt{d1}*x1,\sqrt{d2}*y1} \right)^{T}\) .
The flag = param[0] defines the following predefined values for the matrix \(H\) entries
|
|
|
|
|---|---|---|---|
\(\begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \\ \end{pmatrix}\) |
\(\begin{pmatrix} {1.0} & h_{12} \\ h_{21} & {1.0} \\ \end{pmatrix}\) |
\(\begin{pmatrix} h_{11} & {1.0} \\ {- 1.0} & h_{22} \\ \end{pmatrix}\) |
\(\begin{pmatrix} {1.0} & {0.0} \\ {0.0} & {1.0} \\ \end{pmatrix}\) |
Notice that the values -1.0, 0.0 and 1.0 implied by the flag are not stored in param.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
host or device |
in/out |
<type> scalar that is overwritten on exit. |
|
host or device |
in/out |
<type> scalar that is overwritten on exit. |
|
host or device |
in/out |
<type> scalar that is overwritten on exit. |
|
host or device |
input |
<type> scalar. |
|
host or device |
output |
<type> vector of 5 elements, where |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.12. cublas<t>scal()
cublasStatus_t cublasSscal(cublasHandle_t handle, int n,
const float *alpha,
float *x, int incx)
cublasStatus_t cublasDscal(cublasHandle_t handle, int n,
const double *alpha,
double *x, int incx)
cublasStatus_t cublasCscal(cublasHandle_t handle, int n,
const cuComplex *alpha,
cuComplex *x, int incx)
cublasStatus_t cublasCsscal(cublasHandle_t handle, int n,
const float *alpha,
cuComplex *x, int incx)
cublasStatus_t cublasZscal(cublasHandle_t handle, int n,
const cuDoubleComplex *alpha,
cuDoubleComplex *x, int incx)
cublasStatus_t cublasZdscal(cublasHandle_t handle, int n,
const double *alpha,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function scales the vector x by the scalar \(\alpha\) and overwrites it with the result. Hence, the performed operation is \(\mathbf{x}\lbrack j\rbrack = \alpha \times \mathbf{x}\lbrack j\rbrack\) for \(i = 1,\ldots,n\) and \(j = 1 + \left( {i - 1} \right)*\text{incx}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
input |
Number of elements in the vector |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.5.13. cublas<t>swap()
cublasStatus_t cublasSswap(cublasHandle_t handle, int n, float *x,
int incx, float *y, int incy)
cublasStatus_t cublasDswap(cublasHandle_t handle, int n, double *x,
int incx, double *y, int incy)
cublasStatus_t cublasCswap(cublasHandle_t handle, int n, cuComplex *x,
int incx, cuComplex *y, int incy)
cublasStatus_t cublasZswap(cublasHandle_t handle, int n, cuDoubleComplex *x,
int incx, cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function interchanges the elements of vector x and y. Hence, the performed operation is \(\left. \mathbf{y}\lbrack j\rbrack\Leftrightarrow\mathbf{x}\lbrack k\rbrack \right.\) for \(i = 1,\ldots,n\) , \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6. cuBLAS Level-2 Function Reference
In this chapter we describe the Level-2 Basic Linear Algebra Subprograms (BLAS2) functions that perform matrix-vector operations.
2.6.1. cublas<t>gbmv()
cublasStatus_t cublasSgbmv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n, int kl, int ku,
const float *alpha,
const float *A, int lda,
const float *x, int incx,
const float *beta,
float *y, int incy)
cublasStatus_t cublasDgbmv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n, int kl, int ku,
const double *alpha,
const double *A, int lda,
const double *x, int incx,
const double *beta,
double *y, int incy)
cublasStatus_t cublasCgbmv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n, int kl, int ku,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *x, int incx,
const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZgbmv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n, int kl, int ku,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the banded matrix-vector multiplication
\(\mathbf{y} = \alpha\text{ op}(A)\mathbf{x} + \beta\mathbf{y}\)
where \(A\) is a banded matrix with \(kl\) subdiagonals and \(ku\) superdiagonals, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars. Also, for matrix \(A\)
\(\text{ op}(A) = \begin{cases} A & \text{ if trans == $\mathrm{CUBLAS\_OP\_N}$} \\ A^{T} & \text{ if trans == $\mathrm{CUBLAS\_OP\_T}$} \\ A^{H} & \text{ if trans == $\mathrm{CUBLAS\_OP\_C}$} \\ \end{cases}\)
The banded matrix \(A\) is stored column by column, with the main diagonal stored in row \(ku + 1\) (starting in first position), the first superdiagonal stored in row \(ku\) (starting in second position), the first subdiagonal stored in row \(ku + 2\) (starting in first position), etc. So that in general, the element \(A\left( {i,j} \right)\) is stored in the memory location A(ku+1+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \left\lbrack {\max\left( {1,j - ku} \right),\min\left( {m,j + kl} \right)} \right\rbrack\) . Also, the elements in the array \(A\) that do not conceptually correspond to the elements in the banded matrix (the top left \(ku \times ku\) and bottom right \(kl \times kl\) triangles) are not referenced.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
input |
Number of subdiagonals of matrix |
|
|
input |
Number of superdiagonals of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.2. cublas<t>gemv()
cublasStatus_t cublasSgemv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const float *A, int lda,
const float *x, int incx,
const float *beta,
float *y, int incy)
cublasStatus_t cublasDgemv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const double *alpha,
const double *A, int lda,
const double *x, int incx,
const double *beta,
double *y, int incy)
cublasStatus_t cublasCgemv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *x, int incx,
const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZgemv(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the matrix-vector multiplication
\(\textbf{y} = \alpha\text{ op}(A)\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(m \times n\) matrix stored in column-major format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars. Also, for matrix \(A\)
\(\text{ op}(A) = \begin{cases} A & \text{ if trans == $\mathrm{CUBLAS\_OP\_N}$} \\ A^{T} & \text{ if trans == $\mathrm{CUBLAS\_OP\_T}$} \\ A^{H} & \text{ if trans == $\mathrm{CUBLAS\_OP\_C}$} \\ \end{cases}\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector at least |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector at least |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The parameters |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.3. cublas<t>ger()
cublasStatus_t cublasSger(cublasHandle_t handle, int m, int n,
const float *alpha,
const float *x, int incx,
const float *y, int incy,
float *A, int lda)
cublasStatus_t cublasDger(cublasHandle_t handle, int m, int n,
const double *alpha,
const double *x, int incx,
const double *y, int incy,
double *A, int lda)
cublasStatus_t cublasCgeru(cublasHandle_t handle, int m, int n,
const cuComplex *alpha,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *A, int lda)
cublasStatus_t cublasCgerc(cublasHandle_t handle, int m, int n,
const cuComplex *alpha,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *A, int lda)
cublasStatus_t cublasZgeru(cublasHandle_t handle, int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *A, int lda)
cublasStatus_t cublasZgerc(cublasHandle_t handle, int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *A, int lda)
This function supports the 64-bit Integer Interface.
This function performs the rank-1 update
\(A = \begin{cases} {\alpha\mathbf{xy}^{T} + A} & \text{if ger(),geru() is called} \\ {\alpha\mathbf{xy}^{H} + A} & \text{if gerc() is called} \\ \end{cases}\)
where \(A\) is a \(m \times n\) matrix stored in column-major format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) is a scalar.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.4. cublas<t>sbmv()
cublasStatus_t cublasSsbmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, int k, const float *alpha,
const float *A, int lda,
const float *x, int incx,
const float *beta, float *y, int incy)
cublasStatus_t cublasDsbmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, int k, const double *alpha,
const double *A, int lda,
const double *x, int incx,
const double *beta, double *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the symmetric banded matrix-vector multiplication
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(n \times n\) symmetric banded matrix with \(k\) subdiagonals and superdiagonals, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
If uplo == CUBLAS_FILL_MODE_LOWER then the symmetric banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row 1, the first subdiagonal in row 2 (starting at first position), the second subdiagonal in row 3 (starting at first position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack j,\min(m,j + k)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the bottom right \(k \times k\) triangle) are not referenced.
If uplo == CUBLAS_FILL_MODE_UPPER then the symmetric banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row k + 1, the first superdiagonal in row k (starting at second position), the second superdiagonal in row k-1 (starting at third position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+k+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack\max(1,j - k),j\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the top left \(k \times k\) triangle) are not referenced.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
input |
Number of sub- and super-diagonals of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.5. cublas<t>spmv()
cublasStatus_t cublasSspmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha, const float *AP,
const float *x, int incx, const float *beta,
float *y, int incy)
cublasStatus_t cublasDspmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha, const double *AP,
const double *x, int incx, const double *beta,
double *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the symmetric packed matrix-vector multiplication
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(n \times n\) symmetric matrix stored in packed format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix \(A\) lower or upper part is stored, the other symmetric part is not referenced and is inferred from the stored elements. |
|
|
input |
Number of rows and columns of matrix \(A\) . |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array with \(A\) stored in packed format. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.6. cublas<t>spr()
cublasStatus_t cublasSspr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const float *x, int incx, float *AP)
cublasStatus_t cublasDspr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const double *x, int incx, double *AP)
This function supports the 64-bit Integer Interface.
This function performs the packed symmetric rank-1 update
\(A = \alpha\textbf{x}\textbf{x}^{T} + A\)
where \(A\) is a \(n \times n\) symmetric matrix stored in packed format, \(\mathbf{x}\) is a vector, and \(\alpha\) is a scalar.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix \(A\) lower or upper part is stored, the other symmetric part is not referenced and is inferred from the stored elements. |
|
|
input |
Number of rows and columns of matrix \(A\) . |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array with \(A\) stored in packed format. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.7. cublas<t>spr2()
cublasStatus_t cublasSspr2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const float *x, int incx,
const float *y, int incy, float *AP)
cublasStatus_t cublasDspr2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const double *x, int incx,
const double *y, int incy, double *AP)
This function supports the 64-bit Integer Interface.
This function performs the packed symmetric rank-2 update
\(A = \alpha\left( {\textbf{x}\textbf{y}^{T} + \textbf{y}\textbf{x}^{T}} \right) + A\)
where \(A\) is a \(n \times n\) symmetric matrix stored in packed format, \(\mathbf{x}\) is a vector, and \(\alpha\) is a scalar.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix \(A\) lower or upper part is stored, the other symmetric part is not referenced and is inferred from the stored elements. |
|
|
input |
Number of rows and columns of matrix \(A\) . |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array with \(A\) stored in packed format. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.8. cublas<t>symv()
cublasStatus_t cublasSsymv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const float *A, int lda,
const float *x, int incx, const float *beta,
float *y, int incy)
cublasStatus_t cublasDsymv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const double *A, int lda,
const double *x, int incx, const double *beta,
double *y, int incy)
cublasStatus_t cublasCsymv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha, /* host or device pointer */
const cuComplex *A, int lda,
const cuComplex *x, int incx, const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZsymv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx, const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the symmetric matrix-vector multiplication.
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\) where \(A\) is a \(n \times n\) symmetric matrix stored in lower or upper mode, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
This function has an alternate faster implementation using atomics that can be enabled with cublasSetAtomicsMode().
Please see the section on the function cublasSetAtomicsMode() for more details about the usage of atomics.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix lower or upper part is stored, the other symmetric part is not referenced and is inferred from the stored elements. |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.9. cublas<t>syr()
cublasStatus_t cublasSsyr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const float *x, int incx, float *A, int lda)
cublasStatus_t cublasDsyr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const double *x, int incx, double *A, int lda)
cublasStatus_t cublasCsyr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha,
const cuComplex *x, int incx, cuComplex *A, int lda)
cublasStatus_t cublasZsyr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx, cuDoubleComplex *A, int lda)
This function supports the 64-bit Integer Interface.
This function performs the symmetric rank-1 update
\(A = \alpha\textbf{x}\textbf{x}^{T} + A\)
where \(A\) is a \(n \times n\) symmetric matrix stored in column-major format, \(\mathbf{x}\) is a vector, and \(\alpha\) is a scalar.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.10. cublas<t>syr2()
cublasStatus_t cublasSsyr2(cublasHandle_t handle, cublasFillMode_t uplo, int n,
const float *alpha, const float *x, int incx,
const float *y, int incy, float *A, int lda
cublasStatus_t cublasDsyr2(cublasHandle_t handle, cublasFillMode_t uplo, int n,
const double *alpha, const double *x, int incx,
const double *y, int incy, double *A, int lda
cublasStatus_t cublasCsyr2(cublasHandle_t handle, cublasFillMode_t uplo, int n,
const cuComplex *alpha, const cuComplex *x, int incx,
const cuComplex *y, int incy, cuComplex *A, int lda
cublasStatus_t cublasZsyr2(cublasHandle_t handle, cublasFillMode_t uplo, int n,
const cuDoubleComplex *alpha, const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy, cuDoubleComplex *A, int lda
This function supports the 64-bit Integer Interface.
This function performs the symmetric rank-2 update
\(A = \alpha\left( {\textbf{x}\textbf{y}^{T} + \textbf{y}\textbf{x}^{T}} \right) + A\)
where \(A\) is a \(n \times n\) symmetric matrix stored in column-major format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) is a scalar.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.11. cublas<t>tbmv()
cublasStatus_t cublasStbmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const float *A, int lda,
float *x, int incx)
cublasStatus_t cublasDtbmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const double *A, int lda,
double *x, int incx)
cublasStatus_t cublasCtbmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const cuComplex *A, int lda,
cuComplex *x, int incx)
cublasStatus_t cublasZtbmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const cuDoubleComplex *A, int lda,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function performs the triangular banded matrix-vector multiplication
\(\textbf{x} = \text{op}(A)\textbf{x}\)
where \(A\) is a triangular banded matrix, and \(\mathbf{x}\) is a vector. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
If uplo == CUBLAS_FILL_MODE_LOWER then the triangular banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row 1, the first subdiagonal in row 2 (starting at first position), the second subdiagonal in row 3 (starting at first position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack j,\min(m,j + k)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the bottom right \(k \times k\) triangle) are not referenced.
If uplo == CUBLAS_FILL_MODE_UPPER then the triangular banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row k + 1, the first superdiagonal in row k (starting at second position), the second superdiagonal in row k-1 (starting at third position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+k+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack\max(1,j - k,j)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the top left \(k \times k\) triangle) are not referenced.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
input |
Number of sub- and super-diagonals of matrix . |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The allocation of internal scratch memory failed |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.12. cublas<t>tbsv()
cublasStatus_t cublasStbsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const float *A, int lda,
float *x, int incx)
cublasStatus_t cublasDtbsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const double *A, int lda,
double *x, int incx)
cublasStatus_t cublasCtbsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const cuComplex *A, int lda,
cuComplex *x, int incx)
cublasStatus_t cublasZtbsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, int k, const cuDoubleComplex *A, int lda,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function solves the triangular banded linear system with a single right-hand-side
\(\text{op}(A)\textbf{x} = \textbf{b}\)
where \(A\) is a triangular banded matrix, and \(\mathbf{x}\) and \(\mathbf{b}\) are vectors. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(\mathbf{x}\) overwrites the right-hand-sides \(\mathbf{b}\) on exit.
No test for singularity or near-singularity is included in this function.
If uplo == CUBLAS_FILL_MODE_LOWER then the triangular banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row 1, the first subdiagonal in row 2 (starting at first position), the second subdiagonal in row 3 (starting at first position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack j,\min(m,j + k)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the bottom right \(k \times k\) triangle) are not referenced.
If uplo == CUBLAS_FILL_MODE_UPPER then the triangular banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row k + 1, the first superdiagonal in row k (starting at second position), the second superdiagonal in row k-1 (starting at third position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+k+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack\max(1,j - k,j)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the top left \(k \times k\) triangle) are not referenced.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
input |
Number of sub- and super-diagonals of matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.13. cublas<t>tpmv()
cublasStatus_t cublasStpmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const float *AP,
float *x, int incx)
cublasStatus_t cublasDtpmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const double *AP,
double *x, int incx)
cublasStatus_t cublasCtpmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuComplex *AP,
cuComplex *x, int incx)
cublasStatus_t cublasZtpmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuDoubleComplex *AP,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function performs the triangular packed matrix-vector multiplication
\(\textbf{x} = \text{op}(A)\textbf{x}\)
where \(A\) is a triangular matrix stored in packed format, and \(\mathbf{x}\) is a vector. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the triangular matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the triangular matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(A(i,j)\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array with \(A\) stored in packed format. |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The allocation of internal scratch memory failed |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.14. cublas<t>tpsv()
cublasStatus_t cublasStpsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const float *AP,
float *x, int incx)
cublasStatus_t cublasDtpsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const double *AP,
double *x, int incx)
cublasStatus_t cublasCtpsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuComplex *AP,
cuComplex *x, int incx)
cublasStatus_t cublasZtpsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuDoubleComplex *AP,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function solves the packed triangular linear system with a single right-hand-side
\(\text{op}(A)\textbf{x} = \textbf{b}\)
where \(A\) is a triangular matrix stored in packed format, and \(\mathbf{x}\) and \(\mathbf{b}\) are vectors. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(\mathbf{x}\) overwrites the right-hand-sides \(\mathbf{b}\) on exit.
No test for singularity or near-singularity is included in this function.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the triangular matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the triangular matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix are unity and should not be accessed. |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array with \(A\) stored in packed format. |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.15. cublas<t>trmv()
cublasStatus_t cublasStrmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const float *A, int lda,
float *x, int incx)
cublasStatus_t cublasDtrmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const double *A, int lda,
double *x, int incx)
cublasStatus_t cublasCtrmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuComplex *A, int lda,
cuComplex *x, int incx)
cublasStatus_t cublasZtrmv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuDoubleComplex *A, int lda,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function performs the triangular matrix-vector multiplication
\(\textbf{x} = \text{op}(A)\textbf{x}\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, and \(\mathbf{x}\) is a vector. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The allocation of internal scratch memory failed |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.16. cublas<t>trsv()
cublasStatus_t cublasStrsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const float *A, int lda,
float *x, int incx)
cublasStatus_t cublasDtrsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const double *A, int lda,
double *x, int incx)
cublasStatus_t cublasCtrsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuComplex *A, int lda,
cuComplex *x, int incx)
cublasStatus_t cublasZtrsv(cublasHandle_t handle, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int n, const cuDoubleComplex *A, int lda,
cuDoubleComplex *x, int incx)
This function supports the 64-bit Integer Interface.
This function solves the triangular linear system with a single right-hand-side
\(\text{op}(A)\textbf{x} = \textbf{b}\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, and \(\mathbf{x}\) and \(\mathbf{b}\) are vectors. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(\mathbf{x}\) overwrites the right-hand-sides \(\mathbf{b}\) on exit.
No test for singularity or near-singularity is included in this function.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.17. cublas<t>hemv()
cublasStatus_t cublasChemv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *x, int incx,
const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZhemv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian matrix-vector multiplication
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in lower or upper mode, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
This function has an alternate faster implementation using atomics that can be enabled with
Please see the section on the for more details about the usage of atomics
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.18. cublas<t>hbmv()
cublasStatus_t cublasChbmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, int k, const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *x, int incx,
const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZhbmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, int k, const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian banded matrix-vector multiplication
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(n \times n\) Hermitian banded matrix with \(k\) subdiagonals and superdiagonals, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
If uplo == CUBLAS_FILL_MODE_LOWER then the Hermitian banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row 1, the first subdiagonal in row 2 (starting at first position), the second subdiagonal in row 3 (starting at first position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack j,\min(m,j + k)\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the bottom right \(k \times k\) triangle) are not referenced.
If uplo == CUBLAS_FILL_MODE_UPPER then the Hermitian banded matrix \(A\) is stored column by column, with the main diagonal of the matrix stored in row k + 1, the first superdiagonal in row k (starting at second position), the second superdiagonal in row k-1 (starting at third position), etc. So that in general, the element \(A(i,j)\) is stored in the memory location A(1+k+i-j,j) for \(j = 1,\ldots,n\) and \(i \in \lbrack\max(1,j - k),j\rbrack\) . Also, the elements in the array A that do not conceptually correspond to the elements in the banded matrix (the top left \(k \times k\) triangle) are not referenced.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
input |
Number of sub- and super-diagonals of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.19. cublas<t>hpmv()
cublasStatus_t cublasChpmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha,
const cuComplex *AP,
const cuComplex *x, int incx,
const cuComplex *beta,
cuComplex *y, int incy)
cublasStatus_t cublasZhpmv(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *AP,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian packed matrix-vector multiplication
\(\textbf{y} = \alpha A\textbf{x} + \beta\textbf{y}\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in packed format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) and \(\beta\) are scalars.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array with \(A\) stored in packed format. The imaginary parts of the diagonal elements are assumed to be zero. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> vector with |
|
input |
Stride between consecutive elements of |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.20. cublas<t>her()
cublasStatus_t cublasCher(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const cuComplex *x, int incx,
cuComplex *A, int lda)
cublasStatus_t cublasZher(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const cuDoubleComplex *x, int incx,
cuDoubleComplex *A, int lda)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian rank-1 update
\(A = \alpha\textbf{x}\textbf{x}^{H} + A\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in column-major format, \(\mathbf{x}\) is a vector, and \(\alpha\) is a scalar.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.21. cublas<t>her2()
cublasStatus_t cublasCher2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *A, int lda)
cublasStatus_t cublasZher2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *A, int lda)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian rank-2 update
\(A = \alpha\textbf{x}\textbf{y}^{H} + \overset{ˉ}{\alpha}\textbf{y}\textbf{x}^{H} + A\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in column-major format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) is a scalar.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.22. cublas<t>hpr()
cublasStatus_t cublasChpr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const float *alpha,
const cuComplex *x, int incx,
cuComplex *AP)
cublasStatus_t cublasZhpr(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const double *alpha,
const cuDoubleComplex *x, int incx,
cuDoubleComplex *AP)
This function supports the 64-bit Integer Interface.
This function performs the packed Hermitian rank-1 update
\(A = \alpha\textbf{x}\textbf{x}^{H} + A\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in packed format, \(\mathbf{x}\) is a vector, and \(\alpha\) is a scalar.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array with \(A\) stored in packed format. The imaginary parts of the diagonal elements are assumed and set to zero. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.6.23. cublas<t>hpr2()
cublasStatus_t cublasChpr2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuComplex *alpha,
const cuComplex *x, int incx,
const cuComplex *y, int incy,
cuComplex *AP)
cublasStatus_t cublasZhpr2(cublasHandle_t handle, cublasFillMode_t uplo,
int n, const cuDoubleComplex *alpha,
const cuDoubleComplex *x, int incx,
const cuDoubleComplex *y, int incy,
cuDoubleComplex *AP)
This function supports the 64-bit Integer Interface.
This function performs the packed Hermitian rank-2 update
\(A = \alpha\textbf{x}\textbf{y}^{H} + \overset{ˉ}{\alpha}\textbf{y}\textbf{x}^{H} + A\)
where \(A\) is a \(n \times n\) Hermitian matrix stored in packed format, \(\mathbf{x}\) and \(\mathbf{y}\) are vectors, and \(\alpha\) is a scalar.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the Hermitian matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> array with \(A\) stored in packed format. The imaginary parts of the diagonal elements are assumed and set to zero. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
chpr2, zhpr2
2.6.24. cublas<t>gemvBatched()
cublasStatus_t cublasSgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const float *const Aarray[], int lda,
const float *const xarray[], int incx,
const float *beta,
float *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasDgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const double *alpha,
const double *const Aarray[], int lda,
const double *const xarray[], int incx,
const double *beta,
double *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasCgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const cuComplex *alpha,
const cuComplex *const Aarray[], int lda,
const cuComplex *const xarray[], int incx,
const cuComplex *beta,
cuComplex *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasZgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *const Aarray[], int lda,
const cuDoubleComplex *const xarray[], int incx,
const cuDoubleComplex *beta,
cuDoubleComplex *const yarray[], int incy,
int batchCount)
#if defined(__cplusplus)
cublasStatus_t cublasHSHgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const __half *const Aarray[], int lda,
const __half *const xarray[], int incx,
const float *beta,
__half *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasHSSgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const __half *const Aarray[], int lda,
const __half *const xarray[], int incx,
const float *beta,
float *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasTSTgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const __nv_bfloat16 *const Aarray[], int lda,
const __nv_bfloat16 *const xarray[], int incx,
const float *beta,
__nv_bfloat16 *const yarray[], int incy,
int batchCount)
cublasStatus_t cublasTSSgemvBatched(cublasHandle_t handle, cublasOperation_t trans,
int m, int n,
const float *alpha,
const __nv_bfloat16 *const Aarray[], int lda,
const __nv_bfloat16 *const xarray[], int incx,
const float *beta,
float *const yarray[], int incy,
int batchCount)
#endif
This function supports the 64-bit Integer Interface.
This function performs the matrix-vector multiplication of a batch of matrices and vectors. The batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n), leading dimension (lda), increments (incx, incy) and transposition (trans) for their respective A matrix, x and y vectors. The address of the input matrix and vector, and the output vector of each instance of the batch are read from arrays of pointers passed to the function by the caller.
\(\textbf{y}\lbrack i\rbrack = \alpha\text{op}(A\lbrack i\rbrack)\textbf{x}\lbrack i\rbrack + \beta\textbf{y}\lbrack i\rbrack,\text{ for i} \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) is an array of pointers to matrice \(A\lbrack i\rbrack\) stored in column-major format with dimension \(m \times n\) , and \(\textbf{x}\) and \(\textbf{y}\) are arrays of pointers to vectors. Also, for matrix \(A\lbrack i\rbrack\) ,
\(\text{op}(A\lbrack i\rbrack) = \left\{ \begin{matrix} {A\lbrack i\rbrack} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A\lbrack i\rbrack}^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ {A\lbrack i\rbrack}^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Note
\(\textbf{y}\lbrack i\rbrack\) vectors must not overlap, i.e. the individual gemv operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemv() in different CUDA streams, rather than use this API.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
Array of pointers to <type> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
input |
Array of pointers to <type> array, with each dimension All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Stride of each one-dimensional array x[i]. |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
Array of pointers to <type> array. It has dimensions All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Stride of each one-dimensional array y[i]. |
|
|
input |
Number of pointers contained in Aarray, xarray and yarray. |
If math mode enables fast math modes when using cublasSgemvBatched(), pointers (not the pointer arrays) placed in the GPU memory must be properly aligned to avoid misaligned memory access errors. Ideally all pointers are aligned to at least 16 Bytes. Otherwise it is recommended that they meet the following rule:
if
k % 4 == 0then ensureintptr_t(ptr) % 16 == 0,
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.6.25. cublas<t>gemvStridedBatched()
cublasStatus_t cublasSgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const float *alpha,
const float *A, int lda,
long long int strideA,
const float *x, int incx,
long long int stridex,
const float *beta,
float *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasDgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const double *alpha,
const double *A, int lda,
long long int strideA,
const double *x, int incx,
long long int stridex,
const double *beta,
double *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasCgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
long long int strideA,
const cuComplex *x, int incx,
long long int stridex,
const cuComplex *beta,
cuComplex *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasZgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
long long int strideA,
const cuDoubleComplex *x, int incx,
long long int stridex,
const cuDoubleComplex *beta,
cuDoubleComplex *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasHSHgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const float *alpha,
const __half *A, int lda,
long long int strideA,
const __half *x, int incx,
long long int stridex,
const float *beta,
__half *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasHSSgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const float *alpha,
const __half *A, int lda,
long long int strideA,
const __half *x, int incx,
long long int stridex,
const float *beta,
float *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasTSTgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const float *alpha,
const __nv_bfloat16 *A, int lda,
long long int strideA,
const __nv_bfloat16 *x, int incx,
long long int stridex,
const float *beta,
__nv_bfloat16 *y, int incy,
long long int stridey,
int batchCount)
cublasStatus_t cublasTSSgemvStridedBatched(cublasHandle_t handle,
cublasOperation_t trans,
int m, int n,
const float *alpha,
const __nv_bfloat16 *A, int lda,
long long int strideA,
const __nv_bfloat16 *x, int incx,
long long int stridex,
const float *beta,
float *y, int incy,
long long int stridey,
int batchCount)
This function supports the 64-bit Integer Interface.
This function performs the matrix-vector multiplication of a batch of matrices and vectors. The batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n), leading dimension (lda), increments (incx, incy) and transposition (trans) for their respective A matrix, x and y vectors. Input matrix A and vector x, and output vector y for each instance of the batch are located at fixed offsets in number of elements from their locations in the previous instance. Pointers to A matrix, x and y vectors for the first instance are passed to the function by the user along with offsets in number of elements - strideA, stridex and stridey that determine the locations of input matrices and vectors, and output vectors in future instances.
\(\textbf{y} + i*{stridey} = \alpha\text{op}(A + i*{strideA})(\textbf{x} + i*{stridex}) + \beta(\textbf{y} + i*{stridey}),\text{ for i } \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) is an array of pointers to matrix stored in column-major format with dimension \(A\lbrack i\rbrack\) \(m \times n\) , and \(\textbf{x}\) and \(\textbf{y}\) are arrays of pointers to vectors. Also, for matrix \(A\lbrack i\rbrack\)
\(\text{op}(A\lbrack i\rbrack) = \left\{ \begin{matrix} {A\lbrack i\rbrack} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A\lbrack i\rbrack}^{T} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ {A\lbrack i\rbrack}^{H} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Note
\(\textbf{y}\lbrack i\rbrack\) matrices must not overlap, i.e. the individual gemv operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemv() in different CUDA streams, rather than use this API.
Note
In the table below, we use A[i], x[i], y[i] as notation for A matrix, and x and y vectors in the ith instance of the batch, implicitly assuming they are respectively offsets in number of elements strideA, stridex, stridey away from A[i-1], x[i-1], y[i-1]. The unit for the offset is number of elements and must not be zero .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type>* pointer to the A matrix corresponding to the first instance of the batch, with dimensions |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
device |
input |
<type>* pointer to the x vector corresponding to the first instance of the batch, with each dimension |
|
input |
Stride of each one-dimensional array |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type>* pointer to the y vector corresponding to the first instance of the batch, with each dimension |
|
input |
Stride of each one-dimensional array |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
input |
Number of GEMVs to perform in the batch. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.7. cuBLAS Level-3 Function Reference
In this chapter we describe the Level-3 Basic Linear Algebra Subprograms (BLAS3) functions that perform matrix-matrix operations.
2.7.1. cublas<t>gemm()
cublasStatus_t cublasSgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasDgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasCgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
cublasStatus_t cublasHgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const __half *alpha,
const __half *A, int lda,
const __half *B, int ldb,
const __half *beta,
__half *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication
\(C = \alpha\text{op}(A)\text{op}(B) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times k\) , \(\text{op}(B)\) \(k \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
In the case of cublasHgemm() the device does not support math in half precision. |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.2. cublas<t>gemm3m()
cublasStatus_t cublasCgemm3m(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZgemm3m(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the complex matrix-matrix multiplication, using Gauss complexity reduction algorithm. This can lead to an increase in performance up to 25%
\(C = \alpha\text{op}(A)\text{op}(B) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times k\) , \(\text{op}(B)\) \(k \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
Note
These 2 routines are only supported on GPUs with architecture capabilities equal to or greater than 5.0
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
The possible error values returned by this function and their meanings are listed in the following table:
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
|
|
The device has a compute capabilites lower than 5.0. |
|
The function failed to launch on the GPU. |
For references please refer to NETLIB documentation:
2.7.3. cublas<t>gemmBatched()
cublasStatus_t cublasHgemmBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const __half *alpha,
const __half *const Aarray[], int lda,
const __half *const Barray[], int ldb,
const __half *beta,
__half *const Carray[], int ldc,
int batchCount)
cublasStatus_t cublasSgemmBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const float *alpha,
const float *const Aarray[], int lda,
const float *const Barray[], int ldb,
const float *beta,
float *const Carray[], int ldc,
int batchCount)
cublasStatus_t cublasDgemmBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const double *alpha,
const double *const Aarray[], int lda,
const double *const Barray[], int ldb,
const double *beta,
double *const Carray[], int ldc,
int batchCount)
cublasStatus_t cublasCgemmBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *const Aarray[], int lda,
const cuComplex *const Barray[], int ldb,
const cuComplex *beta,
cuComplex *const Carray[], int ldc,
int batchCount)
cublasStatus_t cublasZgemmBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *const Aarray[], int lda,
const cuDoubleComplex *const Barray[], int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *const Carray[], int ldc,
int batchCount)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication of a batch of matrices. The batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. The address of the input matrices and the output matrix of each instance of the batch are read from arrays of pointers passed to the function by the caller.
\(C\lbrack i\rbrack = \alpha\text{op}(A\lbrack i\rbrack)\text{op}(B\lbrack i\rbrack) + \beta C\lbrack i\rbrack,\text{ for i } \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are arrays of pointers to matrices stored in column-major format with dimensions \(\text{op}(A\lbrack i\rbrack)\) \(m \times k\) , \(\text{op}(B\lbrack i\rbrack)\) \(k \times n\) and \(C\lbrack i\rbrack\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B\lbrack i\rbrack)\) is defined similarly for matrix \(B\lbrack i\rbrack\) .
Note
\(C\lbrack i\rbrack\) matrices must not overlap, that is, the individual gemm operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemm() in different CUDA streams, rather than use this API.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
Array of pointers to <type> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
input |
Array of pointers to <type> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
Array of pointers to <type> array. It has dimensions All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
input |
Number of pointers contained in Aarray, Barray and Carray. |
If math mode enables fast math modes when using cublasSgemmBatched(), pointers (not the pointer arrays) placed in the GPU memory must be properly aligned to avoid misaligned memory access errors. Ideally all pointers are aligned to at least 16 Bytes. Otherwise it is recommended that they meet the following rule:
if
k % 4 == 0then ensureintptr_t(ptr) % 16 == 0,
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
|
cublasHgemmBatched() is only supported for GPU with architecture capabilities equal or greater than 5.3 |
2.7.4. cublas<t>gemmStridedBatched()
cublasStatus_t cublasHgemmStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const __half *alpha,
const __half *A, int lda,
long long int strideA,
const __half *B, int ldb,
long long int strideB,
const __half *beta,
__half *C, int ldc,
long long int strideC,
int batchCount)
cublasStatus_t cublasSgemmStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const float *alpha,
const float *A, int lda,
long long int strideA,
const float *B, int ldb,
long long int strideB,
const float *beta,
float *C, int ldc,
long long int strideC,
int batchCount)
cublasStatus_t cublasDgemmStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const double *alpha,
const double *A, int lda,
long long int strideA,
const double *B, int ldb,
long long int strideB,
const double *beta,
double *C, int ldc,
long long int strideC,
int batchCount)
cublasStatus_t cublasCgemmStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
long long int strideA,
const cuComplex *B, int ldb,
long long int strideB,
const cuComplex *beta,
cuComplex *C, int ldc,
long long int strideC,
int batchCount)
cublasStatus_t cublasCgemm3mStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
long long int strideA,
const cuComplex *B, int ldb,
long long int strideB,
const cuComplex *beta,
cuComplex *C, int ldc,
long long int strideC,
int batchCount)
cublasStatus_t cublasZgemmStridedBatched(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m, int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
long long int strideA,
const cuDoubleComplex *B, int ldb,
long long int strideB,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc,
long long int strideC,
int batchCount)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication of a batch of matrices. The batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. Input matrices A, B and output matrix C for each instance of the batch are located at fixed offsets in number of elements from their locations in the previous instance. Pointers to A, B and C matrices for the first instance are passed to the function by the user along with offsets in number of elements - strideA, strideB and strideC that determine the locations of input and output matrices in future instances.
\(C + i*{strideC} = \alpha\text{op}(A + i*{strideA})\text{op}(B + i*{strideB}) + \beta(C + i*{strideC}),\text{ for i } \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are arrays of pointers to matrices stored in column-major format with dimensions \(\text{op}(A\lbrack i\rbrack)\) \(m \times k\) , \(\text{op}(B\lbrack i\rbrack)\) \(k \times n\) and \(C\lbrack i\rbrack\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B\lbrack i\rbrack)\) is defined similarly for matrix \(B\lbrack i\rbrack\) .
Note
\(C\lbrack i\rbrack\) matrices must not overlap, i.e. the individual gemm operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemm() in different CUDA streams, rather than use this API.
Note
In the table below, we use A[i], B[i], C[i] as notation for A, B and C matrices in the ith instance of the batch, implicitly assuming they are respectively offsets in number of elements strideA, strideB, strideC away from A[i-1], B[i-1], C[i-1]. The unit for the offset is number of elements and must not be zero .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type>* pointer to the A matrix corresponding to the first instance of the batch, with dimensions |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
device |
input |
<type>* pointer to the B matrix corresponding to the first instance of the batch, with dimensions |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type>* pointer to the C matrix corresponding to the first instance of the batch, with dimensions |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
input |
Number of GEMMs to perform in the batch. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
|
cublasHgemmStridedBatched() is only supported for GPU with architecture capabilities equal or greater than 5.3 |
2.7.5. cublas<t>gemmGroupedBatched()
cublasStatus_t cublasSgemmGroupedBatched(cublasHandle_t handle,
const cublasOperation_t transa_array[],
const cublasOperation_t transb_array[],
const int m_array[],
const int n_array[],
const int k_array[],
const float alpha_array[],
const float *const Aarray[],
const int lda_array[],
const float *const Barray[],
const int ldb_array[],
const float beta_array[],
float *const Carray[],
const int ldc_array[],
int group_count,
const int group_size[])
cublasStatus_t cublasDgemmGroupedBatched(cublasHandle_t handle,
const cublasOperation_t transa_array[],
const cublasOperation_t transb_array[],
const int m_array[],
const int n_array[],
const int k_array[],
const double alpha_array[],
const double *const Aarray[],
const int lda_array[],
const double *const Barray[],
const int ldb_array[],
const double beta_array[],
double *const Carray[],
const int ldc_array[],
int group_count,
const int group_size[])
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication on groups of matrices. A given group is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. However, the dimensions, leading dimensions, transpositions, and scaling factors (alpha, beta) may vary between groups. The address of the input matrices and the output matrix of each instance of the batch are read from arrays of pointers passed to the function by the caller. This is functionally equivalent to the following:
idx = 0;
for i = 0:group_count - 1
for j = 0:group_size[i] - 1
gemm(transa_array[i], transb_array[i], m_array[i], n_array[i], k_array[i],
alpha_array[i], Aarray[idx], lda_array[i], Barray[idx], ldb_array[i],
beta_array[i], Carray[idx], ldc_array[i]);
idx += 1;
end
end
where \(\text{$\mathrm{alpha\_array}$}\) and \(\text{$\mathrm{beta\_array}$}\) are arrays of scaling factors, and \(\text{Aarray}\), \(\text{Barray}\) and \(\text{Carray}\) are arrays of pointers to matrices stored in column-major format. For a given index, \(\text{idx}\), that is part of group \(i\), the dimensions are:
\(\text{op}(\text{Aarray}\lbrack\text{idx}\rbrack)\): \(\text{$\mathrm{m\_array}$}\lbrack i\rbrack \times \text{$\mathrm{k\_array}$}\lbrack i\rbrack\)
\(\text{op}(\text{Barray}\lbrack\text{idx}\rbrack)\): \(\text{$\mathrm{k\_array}$}\lbrack i\rbrack \times \text{$\mathrm{n\_array}$}\lbrack i\rbrack\)
\(\text{Carray}\lbrack\text{idx}\rbrack\): \(\text{$\mathrm{m\_array}$}\lbrack i\rbrack \times \text{$\mathrm{n\_array}$}\lbrack i\rbrack\)
Note
This API takes arrays of two different lengths. The arrays of dimensions, leading dimensions, transpositions, and scaling factors are of length group_count and the arrays of matrices are of length problem_count where \(\text{$\mathrm{problem\_count}$} = \sum_{i = 0}^{\text{$\mathrm{group\_count}$} - 1} \text{$\mathrm{group\_size}$}\lbrack i\rbrack\)
For matrix \(A[\text{idx}]\) in group \(i\)
\(\text{op}(A[\text{idx}]) = \left\{ \begin{matrix} A[\text{idx}] & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_N}$}} \\ A[\text{idx}]^{T} & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_T}$}} \\ A[\text{idx}]^{H} & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B[\text{idx}])\) is defined similarly for matrix \(B[\text{idx}]\) in group \(i\).
Note
\(C\lbrack\text{idx}\rbrack\) matrices must not overlap, that is, the individual gemm operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemmBatched() in different CUDA streams, rather than use this API.
Param. |
Memory |
In/out |
Meaning |
Array Length |
|---|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
||
|
host |
input |
Operation op( |
group_count |
|
host |
input |
Operation op( |
group_count |
|
host |
input |
Array containing the number of rows of matrix op( |
group_count |
|
host |
input |
Array containing the number of columns of op( |
group_count |
|
host |
input |
Array containing the number of columns of op( |
group_count |
|
host |
input |
Array containing the <type> scalar used for multiplication for each group. |
group_count |
|
device |
input |
Array of pointers to <type> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
device |
input |
Array of pointers to <type> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
host |
input |
Array containing the <type> scalar used for multiplication for each group. |
group_count |
|
device |
in/out |
Array of pointers to <type> array. It has dimensions All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
host |
input |
Number of groups |
|
|
host |
input |
Array containing the number of pointers contained in Aarray, Barray and Carray for each group. |
group_count |
If math mode enables fast math modes when using cublasSgemmGroupedBatched(), pointers (not the pointer arrays) placed in the GPU memory must be properly aligned to avoid misaligned memory access errors. Ideally all pointers are aligned to at least 16 Bytes. Otherwise it is required that they meet the following rule:
if
k % 4 == 0then ensureintptr_t(ptr) % 16 == 0,
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
|
The pointer mode is set to |
2.7.6. cublas<t>symm()
cublasStatus_t cublasSsymm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasDsymm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasCsymm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZsymm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the symmetric matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha AB + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha BA + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a symmetric matrix stored in lower or upper mode, \(B\) and \(C\) are \(m \times n\) matrices, and \(\alpha\) and \(\beta\) are scalars.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.7. cublas<t>syrk()
cublasStatus_t cublasSsyrk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const float *A, int lda,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasDsyrk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const double *A, int lda,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasCsyrk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZsyrk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the symmetric rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix A. |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.8. cublas<t>syr2k()
cublasStatus_t cublasSsyr2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasDsyr2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasCsyr2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZsyr2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the symmetric rank- \(2k\) update
\(C = \alpha(\text{op}(A)\text{op}(B)^{T} + \text{op}(B)\text{op}(A)^{T}) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\text{ and }B^{T}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.9. cublas<t>syrkx()
cublasStatus_t cublasSsyrkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasDsyrkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasCsyrkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZsyrkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs a variation of the symmetric rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(B)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrices \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\text{ and }B^{T}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
This routine can be used when B is in such way that the result is guaranteed to be symmetric. A usual example is when the matrix B is a scaled form of the matrix A: this is equivalent to B being the product of the matrix A and a diagonal matrix. For an efficient computation of the product of a regular matrix with a diagonal matrix, refer to the routine cublas<t>dgmm().
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.10. cublas<t>trmm()
cublasStatus_t cublasStrmm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
float *C, int ldc)
cublasStatus_t cublasDtrmm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
double *C, int ldc)
cublasStatus_t cublasCtrmm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
cuComplex *C, int ldc)
cublasStatus_t cublasZtrmm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the triangular matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha\text{op}(A)B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha B\text{op}(A)} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, \(B\) and \(C\) are \(m \times n\) matrix, and \(\alpha\) is a scalar. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Notice that in order to achieve better parallelism cuBLAS differs from the BLAS API only for this routine. The BLAS API assumes an in-place implementation (with results written back to B), while the cuBLAS API assumes an out-of-place implementation (with results written into C). The application can obtain the in-place functionality of BLAS in the cuBLAS API by passing the address of the matrix B in place of the matrix C. No other overlapping in the input parameters is supported.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication, if |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.11. cublas<t>trsm()
cublasStatus_t cublasStrsm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const float *alpha,
const float *A, int lda,
float *B, int ldb)
cublasStatus_t cublasDtrsm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const double *alpha,
const double *A, int lda,
double *B, int ldb)
cublasStatus_t cublasCtrsm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
cuComplex *B, int ldb)
cublasStatus_t cublasZtrsm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
cuDoubleComplex *B, int ldb)
This function supports the 64-bit Integer Interface.
This function solves the triangular linear system with multiple right-hand-sides
\(\left\{ \begin{matrix} {\text{op}(A)X = \alpha B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {X\text{op}(A) = \alpha B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, \(X\) and \(B\) are \(m \times n\) matrices, and \(\alpha\) is a scalar. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(X\) overwrites the right-hand-sides \(B\) on exit.
No test for singularity or near-singularity is included in this function.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication, if |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
<type> array. It has dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.12. cublas<t>trsmBatched()
cublasStatus_t cublasStrsmBatched( cublasHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
cublasDiagType_t diag,
int m,
int n,
const float *alpha,
const float *const A[],
int lda,
float *const B[],
int ldb,
int batchCount);
cublasStatus_t cublasDtrsmBatched( cublasHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
cublasDiagType_t diag,
int m,
int n,
const double *alpha,
const double *const A[],
int lda,
double *const B[],
int ldb,
int batchCount);
cublasStatus_t cublasCtrsmBatched( cublasHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
cublasDiagType_t diag,
int m,
int n,
const cuComplex *alpha,
const cuComplex *const A[],
int lda,
cuComplex *const B[],
int ldb,
int batchCount);
cublasStatus_t cublasZtrsmBatched( cublasHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
cublasOperation_t trans,
cublasDiagType_t diag,
int m,
int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *const A[],
int lda,
cuDoubleComplex *const B[],
int ldb,
int batchCount);
This function supports the 64-bit Integer Interface.
This function solves an array of triangular linear systems with multiple right-hand-sides
\(\left\{ \begin{matrix} {\text{op}(A\lbrack i\rbrack)X\lbrack i\rbrack = \alpha B\lbrack i\rbrack} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {X\lbrack i\rbrack\text{op}(A\lbrack i\rbrack) = \alpha B\lbrack i\rbrack} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\lbrack i\rbrack\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, \(X\lbrack i\rbrack\) and \(B\lbrack i\rbrack\) are \(m \times n\) matrices, and \(\alpha\) is a scalar. Also, for matrix \(A\)
\(\text{op}(A\lbrack i\rbrack) = \left\{ \begin{matrix} {A\lbrack i\rbrack} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\lbrack i\rbrack} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ {A^{H}\lbrack i\rbrack} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(X\lbrack i\rbrack\) overwrites the right-hand-sides \(B\lbrack i\rbrack\) on exit.
No test for singularity or near-singularity is included in this function.
This function works for any sizes but is intended to be used for matrices of small sizes where the launch overhead is a significant factor. For bigger sizes, it might be advantageous to call batchCount times the regular cublas<t>trsm() within a set of CUDA streams.
The current implementation is limited to devices with compute capability above or equal 2.0.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Indicates if the elements on the main diagonal of matrix |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication, if |
|
device |
input |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
in/out |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
Number of pointers contained in A and B. |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.13. cublas<t>hemm()
cublasStatus_t cublasChemm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZhemm(cublasHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha AB + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha BA + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a Hermitian matrix stored in lower or upper mode, \(B\) and \(C\) are \(m \times n\) matrices, and \(\alpha\) and \(\beta\) are scalars.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
<type> scalar used for multiplication. If |
|
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.14. cublas<t>herk()
cublasStatus_t cublasCherk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const cuComplex *A, int lda,
const float *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZherk(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const cuDoubleComplex *A, int lda,
const double *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
<type> scalar used for multiplication. If |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.15. cublas<t>her2k()
cublasStatus_t cublasCher2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const float *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZher2k(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const double *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the Hermitian rank- \(2k\) update
\(C = \alpha\text{op}(A)\text{op}(B)^{H} + \overset{ˉ}{\alpha}\text{op}(B)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{H}\text{ and }B^{H}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.7.16. cublas<t>herkx()
cublasStatus_t cublasCherkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const float *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasZherkx(cublasHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const double *beta,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs a variation of the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(B)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{H}\text{ and }B^{H}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
This routine can be used when the matrix B is in such way that the result is guaranteed to be hermitian. An usual example is when the matrix B is a scaled form of the matrix A: this is equivalent to B being the product of the matrix A and a diagonal matrix. For an efficient computation of the product of a regular matrix with a diagonal matrix, refer to the routine cublas<t>dgmm().
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
Real scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8. BLAS-like Extension
This section describes the BLAS-extension functions that perform matrix-matrix operations.
2.8.1. cublas<t>geam()
cublasStatus_t cublasSgeam(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n,
const float *alpha,
const float *A, int lda,
const float *beta,
const float *B, int ldb,
float *C, int ldc)
cublasStatus_t cublasDgeam(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n,
const double *alpha,
const double *A, int lda,
const double *beta,
const double *B, int ldb,
double *C, int ldc)
cublasStatus_t cublasCgeam(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *beta ,
const cuComplex *B, int ldb,
cuComplex *C, int ldc)
cublasStatus_t cublasZgeam(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *beta,
const cuDoubleComplex *B, int ldb,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix addition/transposition
\(C = \alpha\text{op}(A) + \beta\text{op}(B)\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times n\) , \(\text{op}(B)\) \(m \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
The operation is out-of-place if C does not overlap A or B.
The in-place mode supports the following two operations,
\(C = \alpha\text{*}C + \beta\text{op}(B)\)
\(C = \alpha\text{op}(A) + \beta\text{*}C\)
For in-place mode, if C == A, ldc == lda and transa == CUBLAS_OP_N. If C === B, ldc == ldb and transb == CUBLAS_OP_N. If the user does not meet above requirements, CUBLAS_STATUS_INVALID_VALUE is returned.
The operation includes the following special cases:
the user can reset matrix C to zero by setting *alpha = beta = 0.
the user can transpose matrix A by setting *alpha = 1 and *beta = 0.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
output |
<type> array of dimensions |
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.8.2. cublas<t>dgmm()
cublasStatus_t cublasSdgmm(cublasHandle_t handle, cublasSideMode_t mode,
int m, int n,
const float *A, int lda,
const float *x, int incx,
float *C, int ldc)
cublasStatus_t cublasDdgmm(cublasHandle_t handle, cublasSideMode_t mode,
int m, int n,
const double *A, int lda,
const double *x, int incx,
double *C, int ldc)
cublasStatus_t cublasCdgmm(cublasHandle_t handle, cublasSideMode_t mode,
int m, int n,
const cuComplex *A, int lda,
const cuComplex *x, int incx,
cuComplex *C, int ldc)
cublasStatus_t cublasZdgmm(cublasHandle_t handle, cublasSideMode_t mode,
int m, int n,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *x, int incx,
cuDoubleComplex *C, int ldc)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {A \times diag(X)} & {\text{if }\textsf{mode == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ {diag(X) \times A} & {\text{if }\textsf{mode == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ \end{matrix} \right.\)
where \(A\) and \(C\) are matrices stored in column-major format with dimensions \(m \times n\) . \(X\) is a vector of size \(n\) if mode == CUBLAS_SIDE_RIGHT and of size \(m\) if mode == CUBLAS_SIDE_LEFT. \(X\) is gathered from one-dimensional array x with stride incx. The absolute value of incx is the stride and the sign of incx is direction of the stride. If incx is positive, then we forward x from the first element. Otherwise, we backward x from the last element. The formula of X is
\(X\lbrack j\rbrack = \left\{ \begin{matrix} {x\lbrack j \times incx\rbrack} & {\text{if }incx \geq 0} \\ {x\lbrack(\chi - 1) \times |incx| - j \times |incx|\rbrack} & {\text{if }incx < 0} \\ \end{matrix} \right.\)
where \(\chi = m\) if mode == CUBLAS_SIDE_LEFT and \(\chi = n\) if mode == CUBLAS_SIDE_RIGHT.
Example 1: if the user wants to perform \(diag(diag(B)) \times A\) , then \(incx = ldb + 1\) where \(ldb\) is leading dimension of matrix B, either row-major or column-major.
Example 2: if the user wants to perform \(\alpha \times A\) , then there are two choices, either cublas<t>geam() with *beta == 0 and transa == CUBLAS_OP_N or cublas<t>dgmm() with incx == 0 and x[0] == alpha.
The operation is out-of-place. The in-place only works if lda == ldc.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Left multiply if |
|
|
input |
Number of rows of matrix |
|
|
input |
Number of columns of matrix |
|
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
One-dimensional <type> array of size |
|
input |
Stride of one-dimensional array |
|
|
device |
in/out |
<type> array of dimensions |
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.8.3. cublas<t>getrfBatched()
cublasStatus_t cublasSgetrfBatched(cublasHandle_t handle,
int n,
float *const Aarray[],
int lda,
int *PivotArray,
int *infoArray,
int batchSize);
cublasStatus_t cublasDgetrfBatched(cublasHandle_t handle,
int n,
double *const Aarray[],
int lda,
int *PivotArray,
int *infoArray,
int batchSize);
cublasStatus_t cublasCgetrfBatched(cublasHandle_t handle,
int n,
cuComplex *const Aarray[],
int lda,
int *PivotArray,
int *infoArray,
int batchSize);
cublasStatus_t cublasZgetrfBatched(cublasHandle_t handle,
int n,
cuDoubleComplex *const Aarray[],
int lda,
int *PivotArray,
int *infoArray,
int batchSize);
Aarray is an array of pointers to matrices stored in column-major format with dimensions nxn and leading dimension lda.
This function performs the LU factorization of each Aarray[i] for i = 0, …, batchSize-1 by the following equation
\(\text{P}\text{*}{Aarray}\lbrack i\rbrack = L\text{*}U\)
where P is a permutation matrix which represents partial pivoting with row interchanges. L is a lower triangular matrix with unit diagonal and U is an upper triangular matrix.
Formally P is written by a product of permutation matrices Pj, for j = 1,2,...,n, say P = P1 * P2 * P3 * .... * Pn. Pj is a permutation matrix which interchanges two rows of vector x when performing Pj*x. Pj can be constructed by j element of PivotArray[i] by the following Matlab code
// In Matlab PivotArray[i] is an array of base-1.
// In C, PivotArray[i] is base-0.
Pj = eye(n);
swap Pj(j,:) and Pj(PivotArray[i][j] ,:)
L and U are written back to original matrix A, and diagonal elements of L are discarded. The L and U can be constructed by the following Matlab code
// A is a matrix of nxn after getrf.
L = eye(n);
for j = 1:n
L(j+1:n,j) = A(j+1:n,j)
end
U = zeros(n);
for i = 1:n
U(i,i:n) = A(i,i:n)
end
If matrix A(=Aarray[i]) is singular, getrf still works and the value of info(=infoArray[i]) reports first row index that LU factorization cannot proceed. If info is k, U(k,k) is zero. The equation P*A == L*U still holds, however L and U reconstruction needs a different Matlab code as follows:
// A is a matrix of nxn after getrf.
// info is k, which means U(k,k) is zero.
L = eye(n);
for j = 1:k-1
L(j+1:n,j) = A(j+1:n,j)
end
U = zeros(n);
for i = 1:k-1
U(i,i:n) = A(i,i:n)
end
for i = k:n
U(i,k:n) = A(i,k:n)
end
This function is intended to be used for matrices of small sizes where the launch overhead is a significant factor.
cublas<t>getrfBatched supports non-pivot LU factorization if PivotArray is NULL.
cublas<t>getrfBatched supports arbitrary dimension.
cublas<t>getrfBatched only supports compute capability 2.0 or above.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of rows and columns of |
|
|
device |
input/output |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of size |
|
device |
output |
Array of size If If If |
|
input |
Number of pointers contained in A |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The parameters |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.4. cublas<t>getrsBatched()
cublasStatus_t cublasSgetrsBatched(cublasHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const float *const Aarray[],
int lda,
const int *devIpiv,
float *const Barray[],
int ldb,
int *info,
int batchSize);
cublasStatus_t cublasDgetrsBatched(cublasHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const double *const Aarray[],
int lda,
const int *devIpiv,
double *const Barray[],
int ldb,
int *info,
int batchSize);
cublasStatus_t cublasCgetrsBatched(cublasHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const cuComplex *const Aarray[],
int lda,
const int *devIpiv,
cuComplex *const Barray[],
int ldb,
int *info,
int batchSize);
cublasStatus_t cublasZgetrsBatched(cublasHandle_t handle,
cublasOperation_t trans,
int n,
int nrhs,
const cuDoubleComplex *const Aarray[],
int lda,
const int *devIpiv,
cuDoubleComplex *const Barray[],
int ldb,
int *info,
int batchSize);
This function solves an array of systems of linear equations of the form:
\(\text{op}(A\lbrack i \rbrack) X\lbrack i\rbrack = B\lbrack i\rbrack\)
where \(A\lbrack i\rbrack\) is a matrix which has been LU factorized with pivoting, \(X\lbrack i\rbrack\) and \(B\lbrack i\rbrack\) are \(n \times {nrhs}\) matrices. Also, for matrix \(A\)
\(\text{op}(A\lbrack i\rbrack) = \left\{ \begin{matrix} {A\lbrack i\rbrack} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\lbrack i\rbrack} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ {A^{H}\lbrack i\rbrack} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
This function is intended to be used for matrices of small sizes where the launch overhead is a significant factor.
cublas<t>getrsBatched() supports non-pivot LU factorization if devIpiv is NULL.
cublas<t>getrsBatched() supports arbitrary dimension.
cublas<t>getrsBatched() only supports compute capability 2.0 or above.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows and columns of |
|
|
input |
Number of columns of |
|
|
device |
input |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
input |
Array of size |
|
device |
input/output |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each solution matrix |
|
|
host |
output |
If If |
|
input |
Number of pointers contained in A |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.5. cublas<t>getriBatched()
cublasStatus_t cublasSgetriBatched(cublasHandle_t handle,
int n,
const float *const Aarray[],
int lda,
int *PivotArray,
float *const Carray[],
int ldc,
int *infoArray,
int batchSize);
cublasStatus_t cublasDgetriBatched(cublasHandle_t handle,
int n,
const double *const Aarray[],
int lda,
int *PivotArray,
double *const Carray[],
int ldc,
int *infoArray,
int batchSize);
cublasStatus_t cublasCgetriBatched(cublasHandle_t handle,
int n,
const cuComplex *const Aarray[],
int lda,
int *PivotArray,
cuComplex *const Carray[],
int ldc,
int *infoArray,
int batchSize);
cublasStatus_t cublasZgetriBatched(cublasHandle_t handle,
int n,
const cuDoubleComplex *const Aarray[],
int lda,
int *PivotArray,
cuDoubleComplex *const Carray[],
int ldc,
int *infoArray,
int batchSize);
Aarray and Carray are arrays of pointers to matrices stored in column-major format with dimensions n*n and leading dimension lda and ldc respectively.
This function performs the inversion of matrices A[i] for i = 0, …, batchSize-1.
Prior to calling cublas<t>getriBatched, the matrix A[i] must be factorized first using the routine cublas<t>getrfBatched. After the call of cublas<t>getrfBatched, the matrix pointing by Aarray[i] will contain the LU factors of the matrix A[i] and the vector pointing by (PivotArray+i) will contain the pivoting sequence.
Following the LU factorization, cublas<t>getriBatched uses forward and backward triangular solvers to complete inversion of matrices A[i] for i = 0, …, batchSize-1. The inversion is out-of-place, so memory space of Carray[i] cannot overlap memory space of Array[i].
Typically all parameters in cublas<t>getrfBatched would be passed into cublas<t>getriBatched. For example,
// step 1: perform in-place LU decomposition, P*A = L*U.
// Aarray[i] is n*n matrix A[i]
cublasDgetrfBatched(handle, n, Aarray, lda, PivotArray, infoArray, batchSize);
// check infoArray[i] to see if factorization of A[i] is successful or not.
// Array[i] contains LU factorization of A[i]
// step 2: perform out-of-place inversion, Carray[i] = inv(A[i])
cublasDgetriBatched(handle, n, Aarray, lda, PivotArray, Carray, ldc, infoArray, batchSize);
// check infoArray[i] to see if inversion of A[i] is successful or not.
The user can check singularity from either cublas<t>getrfBatched or cublas<t>getriBatched.
This function is intended to be used for matrices of small sizes where the launch overhead is a significant factor.
If cublas<t>getrfBatched is performed by non-pivoting, PivotArray of cublas<t>getriBatched should be NULL.
cublas<t>getriBatched supports arbitrary dimension.
cublas<t>getriBatched only supports compute capability 2.0 or above.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of rows and columns of |
|
|
device |
input |
Array of pointers to <type> array, with each array of dimension |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of size |
|
device |
output |
Array of pointers to <type> array, with each array of dimension |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of size If If |
|
input |
Number of pointers contained in A |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.8.6. cublas<t>matinvBatched()
cublasStatus_t cublasSmatinvBatched(cublasHandle_t handle,
int n,
const float *const A[],
int lda,
float *const Ainv[],
int lda_inv,
int *info,
int batchSize);
cublasStatus_t cublasDmatinvBatched(cublasHandle_t handle,
int n,
const double *const A[],
int lda,
double *const Ainv[],
int lda_inv,
int *info,
int batchSize);
cublasStatus_t cublasCmatinvBatched(cublasHandle_t handle,
int n,
const cuComplex *const A[],
int lda,
cuComplex *const Ainv[],
int lda_inv,
int *info,
int batchSize);
cublasStatus_t cublasZmatinvBatched(cublasHandle_t handle,
int n,
const cuDoubleComplex *const A[],
int lda,
cuDoubleComplex *const Ainv[],
int lda_inv,
int *info,
int batchSize);
A and Ainv are arrays of pointers to matrices stored in column-major format with dimensions n*n and leading dimension lda and lda_inv respectively.
This function performs the inversion of matrices A[i] for i = 0, …, batchSize-1.
This function is a short cut of cublas<t>getrfBatched() plus cublas<t>getriBatched(). However it doesn’t work if n is greater than 32. If not, the user has to go through cublas<t>getrfBatched() and cublas<t>getriBatched().
If the matrix A[i] is singular, then info[i] reports singularity, the same as cublas<t>getrfBatched().
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of rows and columns of |
|
|
device |
input |
Array of pointers to <type> array, with each array of dimension |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of pointers to <type> array, with each array of dimension |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of size If If |
|
input |
Number of pointers contained in |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
2.8.7. cublas<t>geqrfBatched()
cublasStatus_t cublasSgeqrfBatched( cublasHandle_t handle,
int m,
int n,
float *const Aarray[],
int lda,
float *const TauArray[],
int *info,
int batchSize);
cublasStatus_t cublasDgeqrfBatched( cublasHandle_t handle,
int m,
int n,
double *const Aarray[],
int lda,
double *const TauArray[],
int *info,
int batchSize);
cublasStatus_t cublasCgeqrfBatched( cublasHandle_t handle,
int m,
int n,
cuComplex *const Aarray[],
int lda,
cuComplex *const TauArray[],
int *info,
int batchSize);
cublasStatus_t cublasZgeqrfBatched( cublasHandle_t handle,
int m,
int n,
cuDoubleComplex *const Aarray[],
int lda,
cuDoubleComplex *const TauArray[],
int *info,
int batchSize);
Aarray is an array of pointers to matrices stored in column-major format with dimensions m x n and leading dimension lda. TauArray is an array of pointers to vectors of dimension of at least max (1, min(m, n).
This function performs the QR factorization of each Aarray[i] for i = 0, ...,batchSize-1 using Householder reflections. Each matrix Q[i] is represented as a product of elementary reflectors and is stored in the lower part of each Aarray[i] as follows :
Q[j] = H[j][1] H[j][2] . . . H[j](k), where k = min(m,n).
Each H[j][i] has the form
H[j][i] = I - tau[j] * v * v'
where tau[j] is a real scalar, and v is a real vector with v(1:i-1) = 0 and v(i) = 1; v(i+1:m) is stored on exit in Aarray[j][i+1:m,i], and tau in TauArray[j][i].
This function is intended to be used for matrices of small sizes where the launch overhead is a significant factor.
cublas<t>geqrfBatched supports arbitrary dimension.
cublas<t>geqrfBatched only supports compute capability 2.0 or above.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of rows |
|
|
input |
Number of columns of |
|
|
device |
input |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
output |
Array of pointers to <type> vector, with each vector of dim. |
|
host |
output |
If If |
|
input |
Number of pointers contained in |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.8. cublas<t>gelsBatched()
cublasStatus_t cublasSgelsBatched( cublasHandle_t handle,
cublasOperation_t trans,
int m,
int n,
int nrhs,
float *const Aarray[],
int lda,
float *const Carray[],
int ldc,
int *info,
int *devInfoArray,
int batchSize );
cublasStatus_t cublasDgelsBatched( cublasHandle_t handle,
cublasOperation_t trans,
int m,
int n,
int nrhs,
double *const Aarray[],
int lda,
double *const Carray[],
int ldc,
int *info,
int *devInfoArray,
int batchSize );
cublasStatus_t cublasCgelsBatched( cublasHandle_t handle,
cublasOperation_t trans,
int m,
int n,
int nrhs,
cuComplex *const Aarray[],
int lda,
cuComplex *const Carray[],
int ldc,
int *info,
int *devInfoArray,
int batchSize );
cublasStatus_t cublasZgelsBatched( cublasHandle_t handle,
cublasOperation_t trans,
int m,
int n,
int nrhs,
cuDoubleComplex *const Aarray[],
int lda,
cuDoubleComplex *const Carray[],
int ldc,
int *info,
int *devInfoArray,
int batchSize );
Aarray is an array of pointers to matrices stored in column-major format. Carray is an array of pointers to matrices stored in column-major format.
This function find the least squares solution of a batch of overdetermined systems: it solves the least squares problem described as follows :
minimize || Carray[i] - Aarray[i]*Xarray[i] || , with i = 0, ...,batchSize-1
On exit, each Aarray[i] is overwritten with their QR factorization and each Carray[i] is overwritten with the least square solution
cublas<t>gelsBatched supports only the non-transpose operation and only solves over-determined systems (m >= n).
cublas<t>gelsBatched only supports compute capability 2.0 or above.
This function is intended to be used for matrices of small sizes where the launch overhead is a significant factor.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Number of rows of each |
|
|
input |
Number of columns of each |
|
|
input |
Number of columns of each |
|
|
device |
input/output |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
device |
input/output |
Array of pointers to <type> array, with each array of dim. |
|
input |
Leading dimension of two-dimensional array used to store each matrix |
|
|
host |
output |
If If |
|
device |
output |
Optional array of integers of dimension batchsize. If non-null, every element of
|
|
input |
Number of pointers contained in Aarray and Carray |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The parameters |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.9. cublas<t>tpttr()
cublasStatus_t cublasStpttr ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const float *AP,
float *A,
int lda );
cublasStatus_t cublasDtpttr ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const double *AP,
double *A,
int lda );
cublasStatus_t cublasCtpttr ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuComplex *AP,
cuComplex *A,
int lda );
cublasStatus_t cublasZtpttr ( cublasHandle_t handle,
cublasFillMode_t uplo
int n,
const cuDoubleComplex *AP,
cuDoubleComplex *A,
int lda );
This function performs the conversion from the triangular packed format to the triangular format
If uplo == CUBLAS_FILL_MODE_LOWER then the elements of AP are copied into the lower triangular part of the triangular matrix A and the upper part of A is left untouched. If uplo == CUBLAS_FILL_MODE_UPPER then the elements of AP are copied into the upper triangular part of the triangular matrix A and the lower part of A is left untouched.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array with \(A\) stored in packed format. |
|
device |
output |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.10. cublas<t>trttp()
cublasStatus_t cublasStrttp ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const float *A,
int lda,
float *AP );
cublasStatus_t cublasDtrttp ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const double *A,
int lda,
double *AP );
cublasStatus_t cublasCtrttp ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuComplex *A,
int lda,
cuComplex *AP );
cublasStatus_t cublasZtrttp ( cublasHandle_t handle,
cublasFillMode_t uplo,
int n,
const cuDoubleComplex *A,
int lda,
cuDoubleComplex *AP );
This function performs the conversion from the triangular format to the triangular packed format
If uplo == CUBLAS_FILL_MODE_LOWER then the lower triangular part of the triangular matrix A is copied into the array AP. If uplo == CUBLAS_FILL_MODE_UPPER then then the upper triangular part of the triangular matrix A is copied into the array AP.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates which matrix |
|
|
input |
Number of rows and columns of matrix |
|
|
device |
input |
<type> array of dimensions |
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
device |
output |
<type> array with |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.11. cublas<t>gemmEx()
cublasStatus_t cublasSgemmEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const float *alpha,
const void *A,
cudaDataType_t Atype,
int lda,
const void *B,
cudaDataType_t Btype,
int ldb,
const float *beta,
void *C,
cudaDataType_t Ctype,
int ldc)
cublasStatus_t cublasCgemmEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const cuComplex *alpha,
const void *A,
cudaDataType_t Atype,
int lda,
const void *B,
cudaDataType_t Btype,
int ldb,
const cuComplex *beta,
void *C,
cudaDataType_t Ctype,
int ldc)
This function supports the 64-bit Integer Interface.
This function is an extension of cublas<t>gemm(). In this function the input matrices and output matrices can have a lower precision but the computation is still done in the type <t>. For example, in the type float for cublasSgemmEx() and in the type cuComplex for cublasCgemmEx().
\(C = \alpha\text{op}(A)\text{op}(B) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times k\) , \(\text{op}(B)\) \(k \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimensions |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
The matrix types combinations supported for cublasSgemmEx() are listed below:
C |
A/B |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
The matrix types combinations supported for cublasCgemmEx() are listed below :
C |
A/B |
|---|---|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
cublasCgemmEx() is only supported for GPU with architecture capabilities equal or greater than 5.0 |
|
The combination of the parameters |
|
|
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
For more information about the numerical behavior of some GEMM algorithms, refer to the GEMM Algorithms Numerical Behavior section.
2.8.12. cublasGemmEx()
cublasStatus_t cublasGemmEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *A,
cudaDataType_t Atype,
int lda,
const void *B,
cudaDataType_t Btype,
int ldb,
const void *beta,
void *C,
cudaDataType_t Ctype,
int ldc,
cublasComputeType_t computeType,
cublasGemmAlgo_t algo)
#if defined(__cplusplus)
cublasStatus_t cublasGemmEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *A,
cudaDataType Atype,
int lda,
const void *B,
cudaDataType Btype,
int ldb,
const void *beta,
void *C,
cudaDataType Ctype,
int ldc,
cudaDataType computeType,
cublasGemmAlgo_t algo)
#endif
This function supports the 64-bit Integer Interface.
This function is an extension of cublas<t>gemm() that allows the user to individually specify the data types for each of the A, B and C matrices, the precision of computation and the GEMM algorithm to be run. Supported combinations of arguments are listed further down in this section.
Note
The second variant of cublasGemmEx() function is provided for backward compatibility with C++ applications code, where the computeType parameter is of cudaDataType instead of cublasComputeType_t. C applications would still compile with the updated function signature.
This function is only supported on devices with compute capability 5.0 or later.
\(C = \alpha\text{op}(A)\text{op}(B) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times k\) , \(\text{op}(B)\) \(k \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
Scaling factor for A*B of the type that corresponds to the computeType and Ctype, see the table below for details. |
|
device |
input |
<type> array of dimensions |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
Scaling factor for C of the type that corresponds to the computeType and Ctype, see the table below for details. If |
|
device |
in/out |
<type> array of dimensions |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of a two-dimensional array used to store the matrix |
|
|
input |
Enumerant specifying the computation type. |
|
|
input |
Enumerant specifying the algorithm. See cublasGemmAlgo_t. |
cublasGemmEx() supports the following Compute Type, Scale Type, Atype/Btype, and Ctype:
Compute Type |
Scale Type (alpha and beta) |
Atype/Btype |
Ctype |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note
CUBLAS_COMPUTE_32I and CUBLAS_COMPUTE_32I_PEDANTIC compute types are only supported with A, B being 4-byte aligned and lda, ldb being multiples of 4. For better performance, it is also recommended that IMMA kernels requirements for a regular data ordering listed here are met.
The possible error values returned by this function and their meanings are listed in the following table.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
cublasGemmEx() is only supported for GPU with architecture capabilities equal or greater than 5.0. |
|
The combination of the parameters |
|
|
|
The function failed to launch on the GPU. |
Starting with release 11.2, using the typed functions instead of the extension functions (cublas**Ex()) helps in reducing the binary size when linking to static cuBLAS Library.
Also refer to: sgemm.()
For more information about the numerical behavior of some GEMM algorithms, refer to the GEMM Algorithms Numerical Behavior section.
2.8.13. cublasGemmBatchedEx()
cublasStatus_t cublasGemmBatchedEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *const Aarray[],
cudaDataType_t Atype,
int lda,
const void *const Barray[],
cudaDataType_t Btype,
int ldb,
const void *beta,
void *const Carray[],
cudaDataType_t Ctype,
int ldc,
int batchCount,
cublasComputeType_t computeType,
cublasGemmAlgo_t algo)
#if defined(__cplusplus)
cublasStatus_t cublasGemmBatchedEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *const Aarray[],
cudaDataType Atype,
int lda,
const void *const Barray[],
cudaDataType Btype,
int ldb,
const void *beta,
void *const Carray[],
cudaDataType Ctype,
int ldc,
int batchCount,
cudaDataType computeType,
cublasGemmAlgo_t algo)
#endif
This function supports the 64-bit Integer Interface.
This function is an extension of cublas<t>gemmBatched() that performs the matrix-matrix multiplication of a batch of matrices and allows the user to individually specify the data types for each of the A, B and C matrix arrays, the precision of computation and the GEMM algorithm to be run. Like cublas<t>gemmBatched(), the batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. The address of the input matrices and the output matrix of each instance of the batch are read from arrays of pointers passed to the function by the caller. Supported combinations of arguments are listed further down in this section.
Note
The second variant of cublasGemmBatchedEx() function is provided for backward compatibility with C++ applications code, where the computeType parameter is of cudaDataType instead of cublasComputeType_t. C applications would still compile with the updated function signature.
\(C\lbrack i\rbrack = \alpha\text{op}(A\lbrack i\rbrack)\text{op}(B\lbrack i\rbrack) + \beta C\lbrack i\rbrack,\text{ for i } \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are arrays of pointers to matrices stored in column-major format with dimensions \(\text{op}(A\lbrack i\rbrack)\) \(m \times k\) , \(\text{op}(B\lbrack i\rbrack)\) \(k \times n\) and \(C\lbrack i\rbrack\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B\lbrack i\rbrack)\) is defined similarly for matrix \(B\lbrack i\rbrack\) .
Note
\(C\lbrack i\rbrack\) matrices must not overlap, i.e. the individual gemm operations must be computable independently; otherwise, behavior is undefined.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemm() in different CUDA streams, rather than use this API.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
Scaling factor for matrix products of the type that corresponds to the computeType and Ctype, see the table below for details. |
|
device |
input |
Array of pointers to <Atype> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
device |
input |
Array of pointers to <Btype> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
Scaling factor for |
|
device |
in/out |
Array of pointers to <Ctype> array. It has dimensions All pointers must meet certain alignment criteria. Please see below for details. |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of a two-dimensional array used to store each matrix |
|
|
input |
Number of pointers contained in |
|
|
input |
Enumerant specifying the computation type. |
|
|
input |
Enumerant specifying the algorithm. See cublasGemmAlgo_t. |
cublasGemmBatchedEx() supports the following Compute Type, Scale Type, Atype/Btype, and Ctype:
Compute Type |
Scale Type (alpha and beta) |
Atype/Btype |
Ctype |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If Atype is CUDA_R_16F or CUDA_R_16BF, or computeType is any of the FAST options, or when math mode or algo enable fast math modes, pointers (not the pointer arrays) placed in the GPU memory must be properly aligned to avoid misaligned memory access errors. Ideally all pointers are aligned to at least 16 Bytes. Otherwise it is recommended that they meet the following rule:
if
k % 8 == 0then ensureintptr_t(ptr) % 16 == 0,if
k % 2 == 0then ensureintptr_t(ptr) % 4 == 0.
Note
Compute types CUBLAS_COMPUTE_32I and CUBLAS_COMPUTE_32I_PEDANTIC are only supported with all pointers A[i], B[i] being 4-byte aligned and lda, ldb being multiples of 4. For a better performance, it is also recommended that IMMA kernels requirements for the regular data ordering listed here are met.
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
cublasGemmBatchedEx() is only supported for GPU with architecture capabilities equal to or greater than 5.0. |
|
The combination of the parameters |
|
|
|
The function failed to launch on the GPU. |
Also refer to: sgemm.()
2.8.14. cublasGemmStridedBatchedEx()
cublasStatus_t cublasGemmStridedBatchedEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *A,
cudaDataType_t Atype,
int lda,
long long int strideA,
const void *B,
cudaDataType_t Btype,
int ldb,
long long int strideB,
const void *beta,
void *C,
cudaDataType_t Ctype,
int ldc,
long long int strideC,
int batchCount,
cublasComputeType_t computeType,
cublasGemmAlgo_t algo)
#if defined(__cplusplus)
cublasStatus_t cublasGemmStridedBatchedEx(cublasHandle_t handle,
cublasOperation_t transa,
cublasOperation_t transb,
int m,
int n,
int k,
const void *alpha,
const void *A,
cudaDataType Atype,
int lda,
long long int strideA,
const void *B,
cudaDataType Btype,
int ldb,
long long int strideB,
const void *beta,
void *C,
cudaDataType Ctype,
int ldc,
long long int strideC,
int batchCount,
cudaDataType computeType,
cublasGemmAlgo_t algo)
#endif
This function supports the 64-bit Integer Interface.
This function is an extension of cublas<t>gemmStridedBatched() that performs the matrix-matrix multiplication of a batch of matrices and allows the user to individually specify the data types for each of the A, B and C matrices, the precision of computation and the GEMM algorithm to be run. Like cublas<t>gemmStridedBatched(), the batch is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. Input matrices A, B and output matrix C for each instance of the batch are located at fixed offsets in number of elements from their locations in the previous instance. Pointers to A, B and C matrices for the first instance are passed to the function by the user along with the offsets in number of elements - strideA, strideB and strideC that determine the locations of input and output matrices in future instances.
Note
The second variant of cublasGemmStridedBatchedEx() function is provided for backward compatibility with C++ applications code, where the computeType parameter is of cudaDataType_t instead of cublasComputeType_t. C applications would still compile with the updated function signature.
\(C + i*{strideC} = \alpha\text{op}(A + i*{strideA})\text{op}(B + i*{strideB}) + \beta(C + i*{strideC}),\text{ for i } \in \lbrack 0,batchCount - 1\rbrack\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are arrays of pointers to matrices stored in column-major format with dimensions \(\text{op}(A\lbrack i\rbrack)\) \(m \times k\) , \(\text{op}(B\lbrack i\rbrack)\) \(k \times n\) and \(C\lbrack i\rbrack\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B\lbrack i\rbrack)\) is defined similarly for matrix \(B\lbrack i\rbrack\) .
Note
\(C\lbrack i\rbrack\) matrices must not overlap, i.e. the individual gemm operations must be computable independently; otherwise, the behavior is undefined.
On certain problem sizes, it might be advantageous to make multiple calls to cublas<t>gemm() in different CUDA streams, rather than use this API.
Note
In the table below, we use A[i], B[i], C[i] as notation for A, B and C matrices in the ith instance of the batch, implicitly assuming they are respectively offsets in number of elements strideA, strideB, strideC away from A[i-1], B[i-1], C[i-1]. The unit for the offset is number of elements and must not be zero .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Operation op( |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
input |
Number of columns of op( |
|
|
host or device |
input |
Scaling factor for A*B of the <Scale Type> that corresponds to the computeType and Ctype, see the table below for details. |
|
device |
input |
Pointer to <Atype> matrix, A, corresponds to the first instance of the batch, with dimensions |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of two-dimensional array used to store the matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
device |
input |
Pointer to <Btype> matrix, B, corresponds to the first instance of the batch, with dimensions |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
host or device |
input |
Scaling factor for C of the <Scale Type> that corresponds to the computeType and Ctype, see the table below for details. If |
|
device |
in/out |
Pointer to <Ctype> matrix, C, corresponds to the first instance of the batch, with dimensions |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Leading dimension of a two-dimensional array used to store each matrix |
|
|
input |
Value of type long long int that gives the offset in number of elements between |
|
|
input |
Number of GEMMs to perform in the batch. |
|
|
input |
Enumerant specifying the computation type. |
|
|
input |
Enumerant specifying the algorithm. See cublasGemmAlgo_t. |
cublasGemmStridedBatchedEx() supports the following Compute Type, Scale Type, Atype/Btype, and Ctype:
Compute Type |
Scale Type (alpha and beta) |
Atype/Btype |
Ctype |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note
Compute types CUBLAS_COMPUTE_32I and CUBLAS_COMPUTE_32I_PEDANTIC are only supported with all pointers A[i], B[i] being 4-byte aligned and lda, ldb being multiples of 4. For a better performance, it is also recommended that IMMA kernels requirements for the regular data ordering listed here are met.
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
cublasGemmBatchedEx() is only supported for GPU with architecture capabilities equal or greater than 5.0. |
|
The combination of the parameters |
|
|
|
The function failed to launch on the GPU |
Also refer to: sgemm.()
2.8.15. cublasGemmGroupedBatchedEx()
cublasStatus_t cublasGemmGroupedBatchedEx(cublasHandle_t handle,
const cublasOperation_t transa_array[],
const cublasOperation_t transb_array[],
const int m_array[],
const int n_array[],
const int k_array[],
const void *alpha_array,
const void *const Aarray[],
cudaDataType_t Atype,
const int lda_array[],
const void *const Barray[],
cudaDataType_t Btype,
const int ldb_array[],
const void *beta_array,
void *const Carray[],
cudaDataType_t Ctype,
const int ldc_array[],
int group_count,
const int group_size[],
cublasComputeType_t computeType)
This function supports the 64-bit Integer Interface.
This function performs the matrix-matrix multiplication on groups of matrices. A given group is considered to be “uniform”, i.e. all instances have the same dimensions (m, n, k), leading dimensions (lda, ldb, ldc) and transpositions (transa, transb) for their respective A, B and C matrices. However, the dimensions, leading dimensions, transpositions, and scaling factors (alpha, beta) may vary between groups. The address of the input matrices and the output matrix of each instance of the batch are read from arrays of pointers passed to the function by the caller. This is functionally equivalent to the following:
idx = 0;
for i = 0:group_count - 1
for j = 0:group_size[i] - 1
gemmEx(transa_array[i], transb_array[i], m_array[i], n_array[i], k_array[i],
alpha_array[i], Aarray[idx], Atype, lda_array[i], Barray[idx], Btype,
ldb_array[i], beta_array[i], Carray[idx], Ctype, ldc_array[i],
computeType, CUBLAS_GEMM_DEFAULT);
idx += 1;
end
end
where \(\text{$\mathrm{alpha\_array}$}\) and \(\text{$\mathrm{beta\_array}$}\) are arrays of scaling factors, and \(\text{Aarray}\), \(\text{Barray}\) and \(\text{Carray}\) are arrays of pointers to matrices stored in column-major format. For a given index, \(\text{idx}\), that is part of group \(i\), the dimensions are:
\(\text{op}(\text{Aarray}\lbrack\text{idx}\rbrack)\): \(\text{$\mathrm{m\_array}$}\lbrack i\rbrack \times \text{$\mathrm{k\_array}$}\lbrack i\rbrack\)
\(\text{op}(\text{Barray}\lbrack\text{idx}\rbrack)\): \(\text{$\mathrm{k\_array}$}\lbrack i\rbrack \times \text{$\mathrm{n\_array}$}\lbrack i\rbrack\)
\(\text{Carray}\lbrack\text{idx}\rbrack\): \(\text{$\mathrm{m\_array}$}\lbrack i\rbrack \times \text{$\mathrm{n\_array}$}\lbrack i\rbrack\)
Note
This API takes arrays of two different lengths. The arrays of dimensions, leading dimensions, transpositions, and scaling factors are of length group_count and the arrays of matrices are of length problem_count where \(\text{$\mathrm{problem\_count}$} = \sum_{i = 0}^{\text{$\mathrm{group\_count}$} - 1} \text{$\mathrm{group\_size}$}\lbrack i\rbrack\)
For matrix \(A[\text{idx}]\) in group \(i\)
\(\text{op}(A[\text{idx}]) = \left\{ \begin{matrix} A[\text{idx}] & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_N}$}} \\ A[\text{idx}]^{T} & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_T}$}} \\ A[\text{idx}]^{H} & {\text{if }\textsf{$\mathrm{transa\_array}\lbrack i\rbrack$ == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B[\text{idx}])\) is defined similarly for matrix \(B[\text{idx}]\) in group \(i\).
Note
\(C\lbrack\text{idx}\rbrack\) matrices must not overlap, that is, the individual gemm operations must be computable independently; otherwise, undefined behavior is expected.
On certain problem sizes, it might be advantageous to make multiple calls to cublasGemmBatchedEx() in different CUDA streams, rather than use this API.
Param. |
Memory |
In/out |
Meaning |
Array Length |
|---|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
||
|
host |
input |
Array containing the operations, op( |
group_count |
|
host |
input |
Array containing the operations, op( |
group_count |
|
host |
input |
Array containing the number of rows of matrix op( |
group_count |
|
host |
input |
Array containing the number of columns of op( |
group_count |
|
host |
input |
Array containing the number of columns of op( |
group_count |
|
host |
input |
Array containing the <Scale Type> scalar used for multiplication for each group. |
group_count |
|
device |
input |
Array of pointers to <Atype> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
input |
Enumerant specifying the datatype of |
||
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
device |
input |
Array of pointers to <Btype> array, with each array of dim. All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
input |
Enumerant specifying the datatype of |
||
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
host |
input |
Array containing the <Scale Type> scalar used for multiplication for each group. |
group_count |
|
device |
in/out |
Array of pointers to <Ctype> array. It has dimensions All pointers must meet certain alignment criteria. Please see below for details. |
problem_count |
|
input |
Enumerant specifying the datatype of |
||
|
host |
input |
Array containing the leading dimensions of two-dimensional arrays used to store each matrix |
group_count |
|
host |
input |
Number of groups |
|
|
host |
input |
Array containing the number of pointers contained in Aarray, Barray and Carray for each group. |
group_count |
|
input |
Enumerant specifying the computation type. |
cublasGemmGroupedBatchedEx() supports the following Compute Type, Scale Type, Atype/Btype, and Ctype:
Compute Type |
Scale Type (alpha and beta) |
Atype/Btype |
Ctype |
|---|---|---|---|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
If Atype is CUDA_R_16F or CUDA_R_16BF or if the computeType is any of the FAST options, pointers (not the pointer arrays) placed in the GPU memory must be properly aligned to avoid misaligned memory access errors. Ideally all pointers are aligned to at least 16 Bytes. Otherwise it is required that they meet the following rule:
if
(k * AtypeSize) % 16 == 0then ensureintptr_t(ptr) % 16 == 0,if
(k * AtypeSize) % 4 == 0then ensureintptr_t(ptr) % 4 == 0.
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
|
|
The function failed to launch on the GPU |
|
|
2.8.16. cublasCsyrkEx()
cublasStatus_t cublasCsyrkEx(cublasHandle_t handle,
cublasFillMode_t uplo,
cublasOperation_t trans,
int n,
int k,
const cuComplex *alpha,
const void *A,
cudaDataType Atype,
int lda,
const cuComplex *beta,
cuComplex *C,
cudaDataType Ctype,
int ldc)
This function supports the 64-bit Integer Interface.
This function is an extension of cublasCsyrk() where the input matrix and output matrix can have a lower precision but the computation is still done in the type cuComplex
This function performs the symmetric rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Note
This routine is only supported on GPUs with architecture capabilities equal to or greater than 5.0
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix A. |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
The matrix types combinations supported for cublasCsyrkEx() are listed below:
A |
C |
|---|---|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
|
|
The combination of the parameters |
|
The device has a compute capability lower than 5.0. |
|
The function failed to launch on the GPU. |
For references please refer to NETLIB documentation:
2.8.17. cublasCsyrk3mEx()
cublasStatus_t cublasCsyrk3mEx(cublasHandle_t handle,
cublasFillMode_t uplo,
cublasOperation_t trans,
int n,
int k,
const cuComplex *alpha,
const void *A,
cudaDataType Atype,
int lda,
const cuComplex *beta,
cuComplex *C,
cudaDataType Ctype,
int ldc)
This function supports the 64-bit Integer Interface.
This function is an extension of cublasCsyrk() where the input matrix and output matrix can have a lower precision but the computation is still done in the type cuComplex. This routine is implemented using the Gauss complexity reduction algorithm which can lead to an increase in performance up to 25%
This function performs the symmetric rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Note
This routine is only supported on GPUs with architecture capabilities equal to or greater than 5.0
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix A. |
|
|
host or device |
input |
<type> scalar used for multiplication. If |
|
device |
in/out |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
The matrix types combinations supported for cublasCsyrk3mEx() are listed below :
A |
C |
|---|---|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
|
|
The combination of the parameters |
|
The device has a compute capability lower than 5.0. |
|
The function failed to launch on the GPU. |
For references please refer to NETLIB documentation:
2.8.18. cublasCherkEx()
cublasStatus_t cublasCherkEx(cublasHandle_t handle,
cublasFillMode_t uplo,
cublasOperation_t trans,
int n,
int k,
const float *alpha,
const void *A,
cudaDataType Atype,
int lda,
const float *beta,
cuComplex *C,
cudaDataType Ctype,
int ldc)
This function supports the 64-bit Integer Interface.
This function is an extension of cublasCherk() where the input matrix and output matrix can have a lower precision but the computation is still done in the type cuComplex
This function performs the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Note
This routine is only supported on GPUs with architecture capabilities equal to or greater than 5.0
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
<type> scalar used for multiplication. If |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
The matrix types combinations supported for cublasCherkEx() are listed in the following table:
A |
C |
|---|---|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
|
|
The combination of the parameters |
|
The device has a compute capability lower than 5.0. |
|
The function failed to launch on the GPU. |
For references please refer to NETLIB documentation:
2.8.19. cublasCherk3mEx()
cublasStatus_t cublasCherk3mEx(cublasHandle_t handle,
cublasFillMode_t uplo,
cublasOperation_t trans,
int n,
int k,
const float *alpha,
const void *A,
cudaDataType Atype,
int lda,
const float *beta,
cuComplex *C,
cudaDataType Ctype,
int ldc)
This function supports the 64-bit Integer Interface.
This function is an extension of cublasCherk() where the input matrix and output matrix can have a lower precision but the computation is still done in the type cuComplex. This routine is implemented using the Gauss complexity reduction algorithm which can lead to an increase in performance up to 25%
This function performs the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Note
This routine is only supported on GPUs with architecture capabilities equal to or greater than 5.0
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Indicates if matrix |
|
|
input |
Operation op( |
|
|
input |
Number of rows of matrix op( |
|
|
input |
Number of columns of matrix op( |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
device |
input |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
|
|
input |
<type> scalar used for multiplication. If |
|
|
device |
in/out |
<type> array of dimension |
|
input |
Enumerant specifying the datatype of matrix |
|
|
input |
Leading dimension of two-dimensional array used to store matrix |
The matrix types combinations supported for cublasCherk3mEx() are listed in the following table:
A |
C |
|---|---|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
|
|
The combination of the parameters |
|
The device has a compute capability lower than 5.0. |
|
The function failed to launch on the GPU. |
For references please refer to NETLIB documentation:
2.8.20. cublasNrm2Ex()
cublasStatus_t cublasNrm2Ex( cublasHandle_t handle,
int n,
const void *x,
cudaDataType xType,
int incx,
void *result,
cudaDataType resultType,
cudaDataType executionType)
This function supports the 64-bit Integer Interface.
This function is an API generalization of the routine cublas<t>nrm2() where input data, output data and compute type can be specified independently.
This function computes the Euclidean norm of the vector x. The code uses a multiphase model of accumulation to avoid intermediate underflow and overflow, with the result being equivalent to \(\sqrt{\sum_{i = 1}^{n}\left( {\mathbf{x}\lbrack j\rbrack \times \mathbf{x}\lbrack j\rbrack} \right)}\) where \(j = 1 + \left( {i - 1} \right)*\text{incx}\) in exact arithmetic. Notice that the last equation reflects 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
device |
input |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting norm, which is set to |
|
input |
Enumerant specifying the datatype of the |
|
|
input |
Enumerant specifying the datatype in which the computation is executed. |
The datatypes combinations currently supported for cublasNrm2Ex() are listed below :
x |
result |
execution |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The reduction buffer could not be allocated |
|
The combination of the parameters |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
2.8.21. cublasAxpyEx()
cublasStatus_t cublasAxpyEx (cublasHandle_t handle,
int n,
const void *alpha,
cudaDataType alphaType,
const void *x,
cudaDataType xType,
int incx,
void *y,
cudaDataType yType,
int incy,
cudaDataType executiontype);
This function supports the 64-bit Integer Interface.
This function is an API generalization of the routine cublas<t>axpy() where input data, output data and compute type can be specified independently.
This function multiplies the vector x by the scalar \(\alpha\) and adds it to the vector y overwriting the latest vector with the result. Hence, the performed operation is \(\mathbf{y}\lbrack j\rbrack = \alpha \times \mathbf{x}\lbrack k\rbrack + \mathbf{y}\lbrack j\rbrack\) for \(i = 1,\ldots,n\) , \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
input |
Enumerant specifying the datatype of scalar |
|
|
device |
input |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
input |
Enumerant specifying the datatype in which the computation is executed. |
The datatypes combinations currently supported for cublasAxpyEx() are listed in the following table:
alpha |
x |
y |
execution |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
The combination of the parameters |
|
The function failed to launch on the GPU. |
|
|
For references please refer to NETLIB documentation:
2.8.22. cublasDotEx()
cublasStatus_t cublasDotEx (cublasHandle_t handle,
int n,
const void *x,
cudaDataType xType,
int incx,
const void *y,
cudaDataType yType,
int incy,
void *result,
cudaDataType resultType,
cudaDataType executionType);
cublasStatus_t cublasDotcEx (cublasHandle_t handle,
int n,
const void *x,
cudaDataType xType,
int incx,
const void *y,
cudaDataType yType,
int incy,
void *result,
cudaDataType resultType,
cudaDataType executionType);
These functions support the 64-bit Integer Interface.
These functions are an API generalization of the routines cublas<t>dot() and cublas<t>dotc() where input data, output data and compute type can be specified independently. Note: cublas<t>dotc() is dot product conjugated, cublas<t>dotu() is dot product unconjugated.
This function computes the dot product of vectors x and y. Hence, the result is \(\sum_{i = 1}^{n}\left( {\mathbf{x}\lbrack k\rbrack \times \mathbf{y}\lbrack j\rbrack} \right)\) where \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that in the first equation the conjugate of the element of vector x should be used if the function name ends in character ‘c’ and that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
input |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
device |
input |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
host or device |
output |
The resulting dot product, which is set to |
|
input |
Enumerant specifying the datatype of the |
|
|
input |
Enumerant specifying the datatype in which the computation is executed. |
The datatypes combinations currently supported for cublasDotEx() and cublasDotcEx() are listed below:
x |
y |
result |
execution |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The possible error values returned by this function and their meanings are listed in the following table:
Error Value |
Meaning |
|---|---|
|
The operation completed successfully. |
|
The library was not initialized. |
|
The reduction buffer could not be allocated. |
|
The combination of the parameters |
|
The function failed to launch on the GPU. |
|
|
For references please refer to NETLIB documentation:
2.8.23. cublasRotEx()
cublasStatus_t cublasRotEx(cublasHandle_t handle,
int n,
void *x,
cudaDataType xType,
int incx,
void *y,
cudaDataType yType,
int incy,
const void *c, /* host or device pointer */
const void *s,
cudaDataType csType,
cudaDataType executiontype);
This function supports the 64-bit Integer Interface.
This function is an extension to the routine cublas<t>rot() where input data, output data, cosine/sine type, and compute type can be specified independently.
This function applies Givens rotation matrix (i.e., rotation in the x,y plane counter-clockwise by angle defined by \(cos(alpha) = c\), \(sin(alpha) = s\)):
\(G = \begin{pmatrix} c & s \\ {- s} & c \\ \end{pmatrix}\)
to vectors x and y.
Hence, the result is \(\mathbf{x}\lbrack k\rbrack = c \times \mathbf{x}\lbrack k\rbrack + s \times \mathbf{y}\lbrack j\rbrack\) and \(\mathbf{y}\lbrack j\rbrack = - s \times \mathbf{x}\lbrack k\rbrack + c \times \mathbf{y}\lbrack j\rbrack\) where \(k = 1 + \left( {i - 1} \right)*\text{incx}\) and \(j = 1 + \left( {i - 1} \right)*\text{incy}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vectors |
|
|
device |
in/out |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
device |
in/out |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
host or device |
input |
Cosine element of the rotation matrix. |
|
host or device |
input |
Sine element of the rotation matrix. |
|
input |
Enumerant specifying the datatype of |
|
|
input |
Enumerant specifying the datatype in which the computation is executed. |
The datatypes combinations currently supported for cublasRotEx() are listed below :
executionType |
xType / yType |
csType |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The function failed to launch on the GPU |
For references please refer to NETLIB documentation:
2.8.24. cublasScalEx()
cublasStatus_t cublasScalEx(cublasHandle_t handle,
int n,
const void *alpha,
cudaDataType alphaType,
void *x,
cudaDataType xType,
int incx,
cudaDataType executionType);
This function supports the 64-bit Integer Interface.
This function scales the vector x by the scalar \(\alpha\) and overwrites it with the result. Hence, the performed operation is \(\mathbf{x}\lbrack j\rbrack = \alpha \times \mathbf{x}\lbrack j\rbrack\) for \(i = 1,\ldots,n\) and \(j = 1 + \left( {i - 1} \right)*\text{incx}\) . Notice that the last two equations reflect 1-based indexing used for compatibility with Fortran.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
Handle to the cuBLAS library context. |
|
|
input |
Number of elements in the vector |
|
|
host or device |
input |
<type> scalar used for multiplication. |
|
input |
Enumerant specifying the datatype of scalar |
|
|
device |
in/out |
<type> vector with |
|
input |
Enumerant specifying the datatype of vector |
|
|
input |
Stride between consecutive elements of |
|
|
input |
Enumerant specifying the datatype in which the computation is executed. |
The datatypes combinations currently supported for cublasScalEx() are listed below :
alpha |
x |
execution |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
The operation completed successfully |
|
The library was not initialized |
|
The combination of the parameters |
|
The function failed to launch on the GPU |
|
|
For references please refer to NETLIB documentation:
3. Using the cuBLASLt API
3.1. General Description
The cuBLASLt library is a new lightweight library dedicated to GEneral Matrix-to-matrix Multiply (GEMM) operations with a new flexible API. This new library adds flexibility in matrix data layouts, input types, compute types, and also in choosing the algorithmic implementations and heuristics through parameter programmability.
Once a set of options for the intended GEMM operation are identified by the user, these options can be used repeatedly for different inputs. This is analogous to how cuFFT and FFTW first create a plan and reuse for same size and type FFTs with different input data.
Note
The cuBLASLt library does not guarantee the support of all possible sizes and configurations, however, since CUDA 12.2 update 2, the problem size limitations on m, n, and batch size have been largely resolved. The main focus of the library is to provide the most performant kernels, which might have some implied limitations. Some non-standard configurations may require a user to handle them manually, typically by decomposing the problem into smaller parts (see Problem Size Limitations).
3.1.1. Problem Size Limitations
There are inherent problem size limitations that are a result of limitations in CUDA grid dimensions. For example, many kernels do not support batch sizes greater than 65535 due to a limitation on the z dimension of a grid. There are similar restriction on the m and n values for a given problem.
In cases where a problem cannot be run by a single kernel, cuBLASLt will attempt to decompose the problem into multiple sub-problems and solve it by running the kernel on each sub-problem.
- There are some restrictions on cuBLASLt internal problem decomposition which are summarized below:
-
Amax computations are not supported. This means that
CUBLASLT_MATMUL_DESC_AMAX_D_POINTERandCUBLASLT_MATMUL_DESC_EPILOGUE_AUX_AMAX_POINTERmust be left unset (see cublasLtMatmulDescAttributes_t)All matrix layouts must have
CUBLASLT_MATRIX_LAYOUT_ORDERset toCUBLASLT_ORDER_COL(see cublasLtOrder_t)cuBLASLt will not partition along the n dimension when
CUBLASLT_MATMUL_DESC_EPILOGUEis set toCUBLASLT_EPILOGUE_DRELU_BGRADorCUBLASLT_EPILOGUE_DGELU_BGRAD(see cublasLtEpilogue_t)
To overcome these limitations, a user may want to partition the problem themself, launch kernels for each sub-problem, and compute any necessary reductions to combine the results.
3.1.2. Heuristics Cache
cuBLASLt uses heuristics to pick the most suitable matmul kernel for execution based on the problem sizes, GPU configuration, and other parameters. This requires performing some computations on the host CPU, which could take tens of microseconds. To overcome this overhead, it is recommended to query the heuristics once using cublasLtMatmulAlgoGetHeuristic() and then reuse the result for subsequent computations using cublasLtMatmul().
For the cases where querying heuristics once and then reusing them is not feasible, cuBLASLt implements a heuristics cache that maps matmul problems to kernels previously selected by heuristics. The heuristics cache uses an LRU-like eviction policy and is thread-safe.
The user can control the heuristics cache capacity with the CUBLASLT_HEURISTICS_CACHE_CAPACITY environment variable or with the cublasLtHeuristicsCacheSetCapacity() function which has higher precedence. The capacity is measured in number of entries and might be rounded up to the nearest multiple of some factor for performance reasons. Each entry takes about 360 bytes but is subject to change. The default capacity is 8192 entries.
Note
Setting capacity to zero disables the cache completely. This can be useful for workloads that do not have a steady state and for which cache operations may have higher overhead than regular heuristics computations.
Note
The cache is not ideal for performance reasons, so it is sometimes necessary to increase its capacity 1.5x-2.x over the anticipated number of unique matmul problems to achieve a nearly perfect hit rate.
See also: cublasLtHeuristicsCacheGetCapacity(), cublasLtHeuristicsCacheSetCapacity().
3.1.3. cuBLASLt Logging
cuBLASLt logging mechanism can be enabled by setting the following environment variables before launching the target application:
-
CUBLASLT_LOG_LEVEL=<level>where<level>is one of the following levels:0- Off - logging is disabled (default)1- Error - only errors will be logged2- Trace - API calls that launch CUDA kernels will log their parameters and important information3- Hints - hints that can potentially improve the application’s performance4- Info - provides general information about the library execution, may contain details about heuristic status5- API Trace - API calls will log their parameter and important information
-
CUBLASLT_LOG_MASK=<mask>, where<mask>is a combination of the following flags:0- Off1- Error2- Trace4- Hints8- Info16- API Trace
For example, use
CUBLASLT_LOG_MASK=5to enable Error and Hints messages. CUBLASLT_LOG_FILE=<file_name>, where<file_name>is a path to a logging file. The file name may contain%i, which will be replaced with the process ID. For examplefile_name_%i.log.
If CUBLASLT_LOG_FILE is not set, the log messages are printed to stdout.
Another option is to use the experimental cuBLASLt logging API. See:
cublasLtLoggerSetCallback(), cublasLtLoggerSetFile(), cublasLtLoggerOpenFile(), cublasLtLoggerSetLevel(), cublasLtLoggerSetMask(), cublasLtLoggerForceDisable()
3.1.4. Narrow Precision Data Types Usage
What we call here narrow precision data types were first introduced as 8-bit floating point data types (FP8) with Ada and Hopper GPUs (compute capability 8.9 and above), and were designed to further accelerate matrix multiplications. There are two types of FP8 available:
CUDA_R_8F_E4M3is designed to be accurate at a smaller dynamic range than half precision. The E4 and M3 indicate a 4-bit exponent and a 3-bit mantissa respectively. For more details, see __nv__fp8_e4m3.CUDA_R_8F_E5M2is designed to be accurate at a similar dynamic range as half precision. The E5 and M2 indicate a 5-bit exponent and a 2-bit mantissa respectively. For more information see __nv__fp8_e5m2.
Note
Unless otherwise stated, FP8 refers to both CUDA_R_8F_E4M3 and CUDA_R_8F_E5M2.
With the Blackwell GPUs (compute capability 10.0 and above), cuBLAS adds support for 4-bit floating data type (FP4) CUDA_R_4F_E2M1. The E2 and M1 indicate a 2-bit exponent and a 1-bit mantissa respectively. For more details, see __nv_fp4_e2m1.
In order to maintain accuracy, data in narrow precisions needs to be scaled or dequantized before and potentially quantized after computations. cuBLAS provides several modes how the scaling factors are applied, defined in cublasLtMatmulMatrixScale_t and configured via the CUBLASLT_MATMUL_DESC_X_SCALE_MODE attributes (here X stands for A, B, C, D, D_OUT, or EPILOGUE_AUX; see cublasLtMatmulDescAttributes_t). The scaling modes overview is given in the next table, and more details are available in the subsequent sections.
Mode |
Supported compute capabilities |
Tensor values data type |
Scaling factors data type |
Scaling factor layout |
|---|---|---|---|---|
8.9+ |
|
|
Scalar |
|
9.0 |
|
|
Vector |
|
9.0 |
|
|
Tensor |
|
9.0 |
|
|
Tensor |
|
10.0+ |
|
|
Tiled tensor 4 |
|
10.0+ |
|
|
Tiled tensor 4 |
|
10.0+ |
|
|
Array of pointers |
NOTES:
- 1(1,2)
-
Scaling factors that have
CUDA_R_32Fdata type can be negative and are applied as-is without taking their absolute value first. - 2
-
CUDA_R_8F_UE8M0is an 8-bit unsigned exponent-only floating data type. For more information see __nv_fp8_e8m0. - 3
-
CUDA_R_8F_UE4M3is an unsigned version ofCUDA_R_E4M3. The sign bit is ignored, so this enumerant is provided for convenience. - 4(1,2)
-
See 1D Block Scaling Factors Layout for more details.
Note
Scales are only applicable to narrow precisions matmuls. If any scale is set for a non-narrow precisions matmul, cuBLAS will return an error. Furthermore, scales are generally only supported for narrow precision tensors. If the corresponding scale is set for a non-narrow precisions tensor, cuBLAS will return an error. The one exception is that the C tensor is allowed to have a scale for non-narrow data types with tensorwide scaling mode.
Note
Only Tensorwide scaling is supported when cublasLtBatchMode_t of any matrix is set to CUBLASLT_BATCH_MODE_POINTER_ARRAY.
3.1.4.1. Tensorwide Scaling For FP8 Data Types
Tensorwide scaling is enabled when CUBLASLT_MATMUL_DESC_X_SCALE_MODE attributes (here X stands for A, B, C, D, or EPILOGUE_AUX; see cublasLtMatmulDescAttributes_t) for all FP8-precision tensors are set to CUBLASLT_MATMUL_MATRIX_SCALE_SCALAR_32F (this is the default value for FP8 tensors). In such case, the matmul operation in cuBLAS is defined in the following way (assuming, for exposition, that all tensors are using an FP8 precision):
Here \(A\), \(B\), and \(C\) are input tensors, and \(scale_A\), \(scale_B\), \(scale_C\), \(scale_D\), \(\alpha\), and \(\beta\) are input scalars. This differs from the other matrix multiplication routines because of this addition of scaling factors for each matrix. The \(scale_A\), \(scale_B\), and \(scale_C\) are used for de-quantization, and \(scale_D\) is used for quantization. Note that all the scaling factors are applied multiplicatively. This means that sometimes it is necessary to use a scaling factor or its reciprocal depending on the context in which it is applied. For more information on FP8, see cublasLtMatmul() and cublasLtMatmulDescAttributes_t.
For such matrix multiplications, epilogues and the absolute maximums of intermediate values are computed as follows:
Here \(Aux\) is an auxiliary output of matmul consisting of the values that are passed to an epilogue function like GELU, \(scale_{Aux}\) is an optional scaling factor that can be applied to \(Aux\), and \(amax_{Aux}\) is the maximum absolute value in \(Aux\) before scaling. For more information, see attributes CUBLASLT_MATMUL_DESC_AMAX_D_POINTER and CUBLASLT_MATMUL_DESC_EPILOGUE_AUX_AMAX_POINTER in cublasLtMatmulDescAttributes_t.
Note
As indicated in equation above, bias is applied before calculating \(Aux_{temp}\).
3.1.4.2. Experimental: Per-batch Tensorwide Scaling For FP8 Data Types
Per-batch Tensorwide scaling is enabled when CUBLASLT_MATMUL_DESC_X_SCALE_MODE attributes (here X stands for A, B, C, D, or EPILOGUE_AUX; see cublasLtMatmulDescAttributes_t) for all FP8-precision tensors are set to CUBLASLT_MATMUL_MATRIX_SCALE_PER_BATCH_SCALAR_32F.
Per-batch Tensorwide scaling is a variant of tensorwide scaling except that each matrix in the batch has its own scaling factor.
When using per-batch Tensorwide scaling, the \(scale_A\), \(scale_B\), \(scale_C\), \(scale_D\), and \(scale_{Aux}\) must be device arrays of pointers of length CUBLASLT_MATRIX_LAYOUT_BATCH_COUNT.
Note
Per-batch Tensorwide scaling is only supported when cublasLtBatchMode_t of all matrices is set to CUBLASLT_BATCH_MODE_GROUPED.
3.1.4.3. Outer Vector Scaling for FP8 Data Types
This scaling mode (also known as channelwise or rowwise scaling) is a refinement of the tensorwide scaling. Instead of multiplying a matrix by a single scalar, a scaling factor is associated with each row of \(A\) and each column of \(B\):
Notably, \(scale_D\) is not supported because the only supported precisions for \(D\) are CUDA_R_16F, CUDA_R_16BF, and CUDA_R_32F.
To enable outer vector scaling, the CUBLASLT_MATMUL_DESC_A_SCALE_MODE and CUBLASLT_MATMUL_DESC_B_SCALE_MODE attributes, must be set to CUBLASLT_MATMUL_MATRIX_SCALE_OUTER_VEC_32F, while all the other scaling modes must not be modified.
When using this scaling mode, the \(scale_A\) and \(scale_B\) must be vectors of length \(M\) and \(N\) respectively.
3.1.4.4. 16/32-Element 1D Block Scaling for FP8 and FP4 Data Types
1D block scaling aims to overcome limitations of having a single scalar to scale a whole tensor. It is described in more details in the OCP MXFP specification, so we give just a brief overview here. Block scaling means that elements within the same 16- or 32-element block of adjacent values are assigned a shared scaling factor.
Currently, block scaling is supported for FP8-precision and FP4-precision tensors and mixing precisions is not supported. To enable block scaling, the CUBLASLT_MATMUL_DESC_X_SCALE_MODE attributes (here X stands for A, B, C, DOUT, or EPILOGUE_AUX; see cublasLtMatmulDescAttributes_t) must be set to CUBLASLT_MATMUL_MATRIX_SCALE_VEC32_UE8M0 for all FP8-precision tensors or to CUBLASLT_MATMUL_MATRIX_SCALE_VEC16_UE4M3 for all FP4-precision tensors.
With block scaling, the matmul operation in cuBLAS is defined in the following way (assuming, for exposition, that all tensors are using a narrow precision). We loosely follow the OCP MXFP specification notation.
First, a scaled block (or an MX-compliant format vector in the OCP MXFP specification) is a tuple \(x = \left(S^x, \left[x^i\right]_{i=1}^k\right)\), where \(S^x\) is a shared scaling factor, and each \(x^i\) is stored using an FP8 or FP4 data type.
A dot product of two scaled blocks \(x = \left(S^x, \left[x^i\right]_{i=1}^{k}\right)\) and \(y = \left(S^y, \left[y^i\right]_{i=1}^{k}\right)\) is defined as follows:
For a sequence of \(n\) blocks \(X = \{x_j\}_{j=1}^n\) and \(Y = \{y_j\}_{j=1}^n\), the generalized dot product is defined as:
The generalized dot product can be used to define the matrix multiplication by combining together one scaling factor per \(k\) elements of \(A\) and \(B\) in the \(K\) dimension (assuming, for simplicity, that \(K\) is divisible by \(k\) without a remainder):
Now, the full matmul can be written as:
The \(Quantize\) is explained in the 1D Block Quantization section, and \(Dequantize\) is defined as:
Note
In addition to \(scale_D^{out}\) that is computed during quantization, there is also an input scalar tensor-wide scaling factor \(scale_D^{in}\) for \(D\) that is available only when scaling factors use the CUDA_R_8F_UE4M3 data type. It is used to ‘compress’ computed values prior to quantization.
3.1.4.4.1. 1D Block Quantization
Consider a single block of \(k\) elements of \(D\) in the \(M\) dimension: \(D^b_{fp32} = \left[d^i_{fp32}\right]_{i=1}^k\). Quantization of partial blocks is performed as if the missing values are zero. Let \(Amax(DType)\) be the maximal value representable in the destination precision.
The following computations steps are common to all combinations of output and scaling factors data types.
Compute the block absolute maximum value \(Amax(D^b_{fp32}) = max(\{|d_i|\}_{i=1}^k)\).
Compute the block scaling factor in single precision as \(S^b_{fp32} = \frac{Amax(D^b_{fp32})}{Amax(DType)}\).
Computing scaling and conversion factors for FP8 with UE8M0 scales
Note
RNE rounding is assumed unless noted otherwise.
Computations consist of the following steps:
Extract the block scaling factor exponent without bias adjustment as an integer \(E^b_{int}\) and mantissa as a fixed point number \(M^b_{fixp}\) from \(S^b_{fp32}\) (the actual implementation operates on bit representation directly).
Round the block exponent up keeping it within the range of values representable in UE8M0: \(E^b_{int} = \left\{\begin{array}{ll} E^b_{int} + 1, & \text{if } S^b_{fp32} \text{ is a normal number and } E^b_{int} < 254 \text{ and } M^b_{fixp} > 0 \\ E^b_{int} + 1, & \text{if } S^b_{fp32} \text{is a denormal number and } M^b_{fixp} > 0.5, \\ E^b_{int}, & \text{otherwise.} \end{array}\right.\)
Compute the block scaling factor as \(S^b_{ue8m0} = 2^{E^b_{int}}\). Note that UE8M0 data type has exponent bias of 127.
Compute the block conversion factor \(R^b_{fp32} = \frac{1}{fp32(S^b_{ue8m0})}\).
Note
The algorithm above differs from the OCP MXFP suggested rounding scheme.
Computing scaling and conversion factors for FP4 with UE4M3 scales
Here we assume that the algorithm is provided with a precomputed input tensorwide scaling factor \(scale_D^{in}\) which in general case is computed as
where \(Amax(D_{temp})\) is a global absolute maximum of matmul results before quantization. Since computing this value requires knowing the result of the whole computation, an approximate value from e.g. the previous iteration is used in practice.
Computations consist of the following steps:
Compute the narrow precision value of the block scaling factor \(S^b_{e4m3} = e4m3(S^b_{fp32})\).
Compute the block conversion factor \(R^b_{fp32} = \frac{1}{fp32(S^b_{e4m3})}\).
Applying conversion factors
For each \(i = 1 \ldots k\), compute \(d^i = DType(d^i_{fp32} \cdot R^b_{fp32})\). The resulting quantized block is \(\left(S^b, \left[d^i\right]_{i=1}^k\right)\), where \(S^b\) is \(S^b_{ue8m0}\) for FP8 with UE8M0 scaling factors, and \(S^b_{ue4m3}\) for FP4 with UE4M3 scaling factors.
3.1.4.4.2. 1D Block Scaling Factors Layout
Scaling factors are stored using a tiled layout. The following figure shows how each 128x4 tile is laid out in memory. The offset in memory is increasing from left to right, and then from top to bottom.
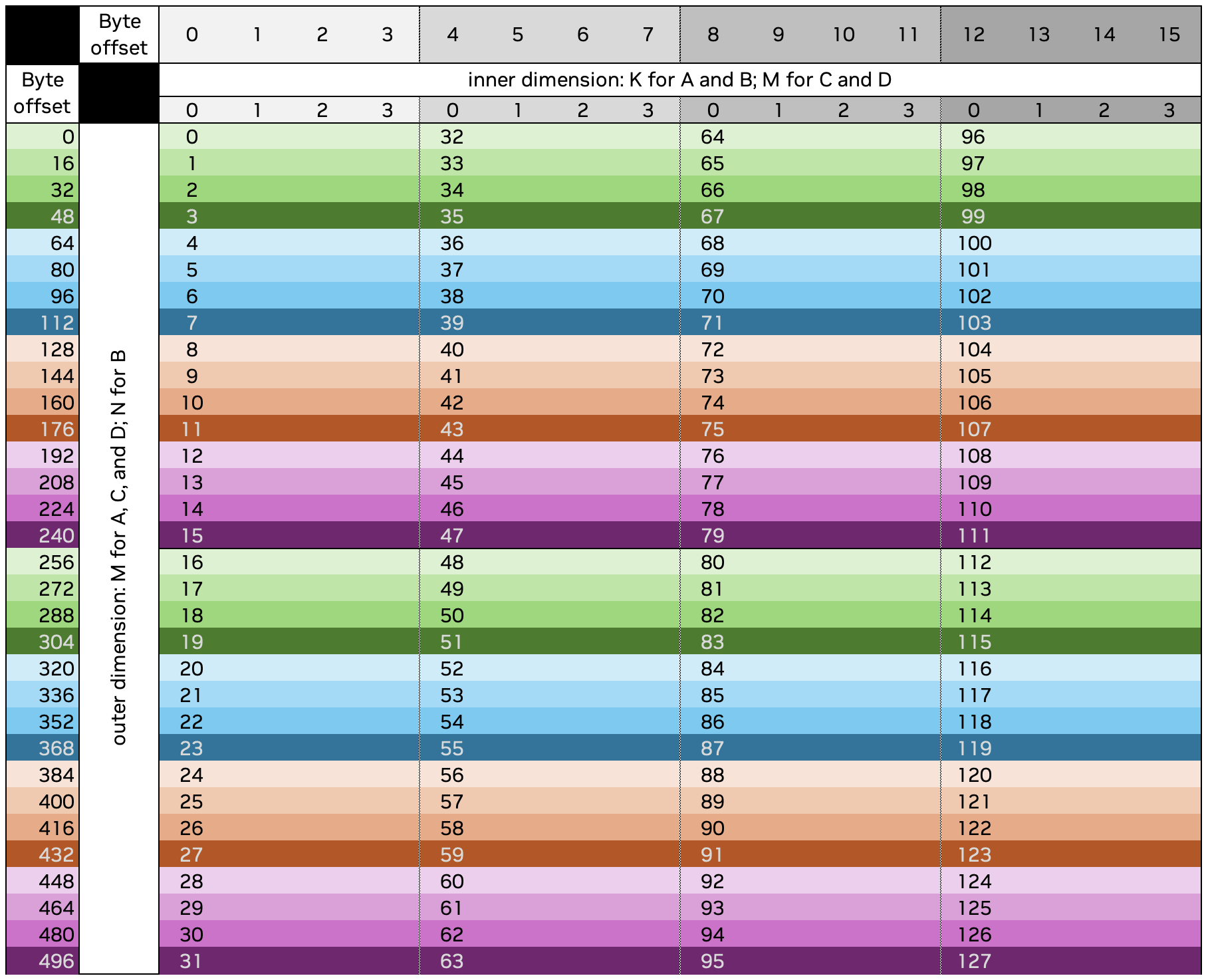
The following pseudocode can be used to translate from inner (K for A and B, and M for C or D) and outer (M for A, and N for B, C and D) indices to linear offset within a tile and back:
// Indices -> offset
offset = (outer % 32) * 16 + (outer / 32) * 4 + inner
// Offset -> Indices
outer = ((offset % 16) / 4) * 32 + (offset / 16)
inner = (offset % 4)
A single tile of scaling factors is applied to a 128x64 block when the scaling mode is CUBLASLT_MATMUL_MATRIX_SCALE_VEC16_UE4M3 and to a 128x128 block when it is CUBLASLT_MATMUL_MATRIX_SCALE_VEC32_UE8M0.
Multiple blocks are arranged in the row-major manner. The next picture shows an example. The offset in memory is increasing from left to right, and then from top to bottom.
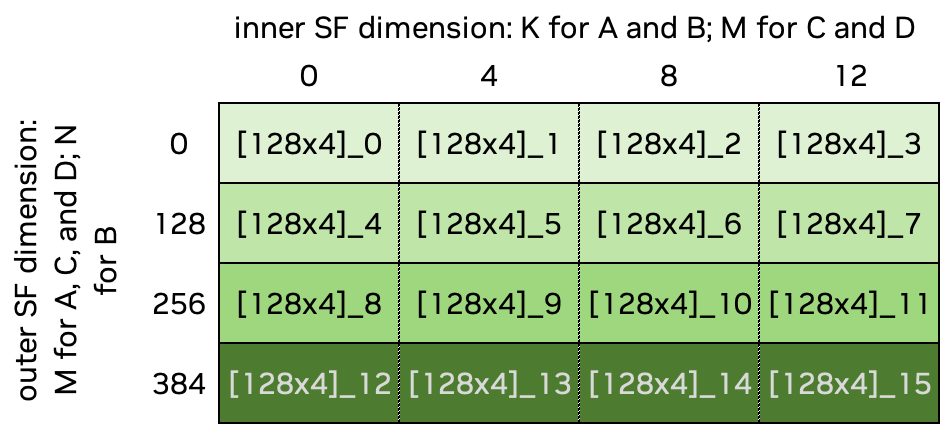
In general, for a scaling factors tensor with sf_inner_dim scaling factors per row, offset of a block with top left coordinate (sf_outer, sf_inner) (using the same correspondence to matrix coordinates as noted above) can be computed using the following pseudocode:
// Indices -> offset
// note that sf_inner is a multiple of 4 due to the tiling layout
offset = (sf_inner + sf_outer * sf_inner_dim) * 128
Note
Starting addresses of scaling factors must be 16B aligned.
Note
Note that the layout described above does not allow transposition. This means that even though the input tensors can be transposed, the layout of scaling factors does not change.
Note
Note that when tensor dimensions are not multiples of the tile size above, it is necessary to still allocate full tile for storage and fill out of bounds values with zeroes. Moreover, when writing output scaling factors, kernels may write additional zeroes, so it is best to not make any assuptions regarding the persistence of out of bounds values.
3.1.4.5. 128-element 1D and 128x128 2D Block Scaling For FP8 Data Types
These two scaling modes apply principles of the scaling approach described 16/32-Element 1D Block Scaling for FP8 and FP4 Data Types to the Hopper GPU architecture. However, here the scaling data type is CUDA_R_32F, and different scaling modes can be used for \(A\) and \(B\), and the only supported precisions for \(D\) are CUDA_R_16F, CUDA_R_16BF, and CUDA_R_32F.
To enable this scaling mode, the CUBLASLT_MATMUL_DESC_X_SCALE_MODE attributes (here X stands for A or B), must be set to CUBLASLT_MATMUL_MATRIX_SCALE_VEC128_32F or CUBLASLT_MATMUL_MATRIX_SCALE_BLK128x128_32F, while all the other scaling modes must not be modified. The following table shows supported combinations:
CUBLASLT_MATMUL_DESC_A_SCALE_MODE |
CUBLASLT_MATMUL_DESC_B_SCALE_MODE |
Supported? |
|---|---|---|
|
|
Yes |
|
|
Yes |
|
|
Yes |
|
|
No |
Using the notation from the 16/32-Element 1D Block Scaling for FP8 and FP4 Data Types, we can define sequences of scaled blocks for the \(i\)-th row of \(A\) in the following way:
Definitions for \(B\) are similar. The matmul is then defined as in 16/32-Element 1D Block Scaling for FP8 and FP4 Data Types with the notable difference that when using the 2D block scaling a single scaling factor is used for the whole 128x128 block of elements.
3.1.4.5.1. Scaling factors layouts
Note
Starting addresses of scaling factors must be 16B aligned.
Note
\(M\) and \(N\) must be multiples of 4.
Then for the CUBLASLT_MATMUL_MATRIX_SCALE_VEC128_32F scaling mode, the scaling factors are:
\(M\)-major for \(A\) with shape \(M \times L\) (\(M\)-major means that elements along the \(M\) dimension are contiguous in memory),
\(N\)-major for \(B\) with shape \(N \times L\).
For the CUBLASLT_MATMUL_MATRIX_SCALE_BLK128x128_32F scaling mode, the scaling factors are \(K\)-major and the stride between the consecutive columns must be a multiple of 4. Let \(L_4 = \lceil L \rceil_4\), where the \(\lceil \cdot \rceil_4\) denotes rounding up to the nearest multiple of 4. Then
for \(A\), the shape of the scaling factors is \(L_4 \times \lceil \frac{M}{128} \rceil\),
for \(B\), the shape of the scaling factors is \(L_4 \times \lceil \frac{N}{128} \rceil\).
3.1.5. Disabling CPU Instructions
As mentioned in the Heuristics Cache section, cuBLASLt heuristics perform some compute-intensive operations on the host CPU. To speed-up the operations, the implementation detects CPU capabilities and may use special instructions, such as Advanced Vector Extensions (AVX) on x86-64 CPUs. However, in some rare cases this might be not desirable. For instance, using advanced instructions may result in CPU running at a lower frequency, which would affect performance of the other host code.
The user can optionally instruct the cuBLASLt library to not use some CPU instructions with the CUBLASLT_DISABLE_CPU_INSTRUCTIONS_MASK environment variable or with the cublasLtDisableCpuInstructionsSetMask() function which has higher precedence.
The default mask is 0, meaning that there are no restrictions.
Please check cublasLtDisableCpuInstructionsSetMask() for more information.
3.2. cuBLASLt Code Examples
Please visit https://github.com/NVIDIA/CUDALibrarySamples/tree/main/cuBLASLt for updated code examples.
3.3. cuBLASLt Datatypes Reference
3.3.1. cublasLtClusterShape_t
cublasLtClusterShape_t is an enumerated type used to configure thread block cluster dimensions. Thread block clusters add an optional hierarchical level and are made up of thread blocks. Similar to thread blocks, these can be one, two, or three-dimensional. See also Thread Block Clusters.
Value |
Description |
|---|---|
|
Cluster shape is automatically selected. |
|
Cluster shape is 1 x 1 x 1. |
|
Cluster shape is 1 x 2 x 1. |
|
Cluster shape is 1 x 4 x 1. |
|
Cluster shape is 2 x 1 x 1. |
|
Cluster shape is 2 x 2 x 1. |
|
Cluster shape is 2 x 4 x 1. |
|
Cluster shape is 4 x 1 x 1. |
|
Cluster shape is 4 x 2 x 1. |
|
Cluster shape is 4 x 4 x 1. |
|
Cluster shape is 1 x 8 x 1. |
|
Cluster shape is 8 x 1 x 1. |
|
Cluster shape is 2 x 8 x 1. |
|
Cluster shape is 8 x 2 x 1. |
|
Cluster shape is 1 x 16 x 1. |
|
Cluster shape is 16 x 1 x 1. |
|
Cluster shape is 1 x 3 x 1. |
|
Cluster shape is 1 x 5 x 1. |
|
Cluster shape is 1 x 6 x 1. |
|
Cluster shape is 1 x 7 x 1. |
|
Cluster shape is 1 x 9 x 1. |
|
Cluster shape is 1 x 10 x 1. |
|
Cluster shape is 1 x 11 x 1. |
|
Cluster shape is 1 x 12 x 1. |
|
Cluster shape is 1 x 13 x 1. |
|
Cluster shape is 1 x 14 x 1. |
|
Cluster shape is 1 x 15 x 1. |
|
Cluster shape is 2 x 3 x 1. |
|
Cluster shape is 2 x 5 x 1. |
|
Cluster shape is 2 x 6 x 1. |
|
Cluster shape is 2 x 7 x 1. |
|
Cluster shape is 3 x 1 x 1. |
|
Cluster shape is 3 x 2 x 1. |
|
Cluster shape is 3 x 3 x 1. |
|
Cluster shape is 3 x 4 x 1. |
|
Cluster shape is 3 x 5 x 1. |
|
Cluster shape is 4 x 3 x 1. |
|
Cluster shape is 5 x 1 x 1. |
|
Cluster shape is 5 x 2 x 1. |
|
Cluster shape is 5 x 3 x 1. |
|
Cluster shape is 6 x 1 x 1. |
|
Cluster shape is 6 x 2 x 1. |
|
Cluster shape is 7 x 1 x 1. |
|
Cluster shape is 7 x 2 x 1. |
|
Cluster shape is 9 x 1 x 1. |
|
Cluster shape is 10 x 1 x 1. |
|
Cluster shape is 11 x 1 x 1. |
|
Cluster shape is 12 x 1 x 1. |
|
Cluster shape is 13 x 1 x 1. |
|
Cluster shape is 14 x 1 x 1. |
|
Cluster shape is 15 x 1 x 1. |
3.3.2. cublasLtEpilogue_t
The cublasLtEpilogue_t is an enum type to set the postprocessing options for the epilogue.
Value |
Description |
|---|---|
|
No special postprocessing, just scale and quantize the results if necessary. |
|
Apply ReLU point-wise transform to the results ( |
|
Apply ReLU point-wise transform to the results ( |
|
Apply (broadcast) bias from the bias vector. Bias vector length must match matrix D rows, and it must be packed (such as stride between vector elements is 1). Bias vector is broadcast to all columns and added before applying the final postprocessing. |
|
Apply bias and then ReLU transform. |
|
Apply bias and then ReLU transform. This epilogue mode produces an extra output, see |
|
Apply ReLu gradient to matmul output. Store ReLu gradient in the output matrix. This epilogue mode requires an extra input, see |
|
Apply independently ReLu and Bias gradient to matmul output. Store ReLu gradient in the output matrix, and Bias gradient in the bias buffer (see |
|
Apply GELU point-wise transform to the results ( |
|
Apply GELU point-wise transform to the results ( |
|
Apply Bias and then GELU transform 5. |
|
Apply Bias and then GELU transform 5. This epilogue mode outputs GELU input as a separate matrix (useful for training). See |
|
Apply GELU gradient to matmul output. Store GELU gradient in the output matrix. This epilogue mode requires an extra input, see |
|
Apply independently GELU and Bias gradient to matmul output. Store GELU gradient in the output matrix, and Bias gradient in the bias buffer (see |
|
Apply Bias gradient to the input matrix A. The bias size corresponds to the number of rows of the matrix D. The reduction happens over the GEMM’s “k” dimension. Store Bias gradient in the bias buffer, see |
|
Apply Bias gradient to the input matrix B. The bias size corresponds to the number of columns of the matrix D. The reduction happens over the GEMM’s “k” dimension. Store Bias gradient in the bias buffer, see |
NOTES:
- 5(1,2)
-
GELU (Gaussian Error Linear Unit) is approximated by: \({0.5}x\left( 1 + \text{tanh}\left( \sqrt{2/\pi}\left( x + {0.044715}x^{3} \right) \right) \right)\)
Note
Only CUBLASLT_EPILOGUE_DEFAULT is supported when cublasLtBatchMode_t of any matrix is set to CUBLASLT_BATCH_MODE_POINTER_ARRAY or CUBLASLT_BATCH_MODE_GROUPED.
3.3.3. cublasLtHandle_t
The cublasLtHandle_t type is a pointer type to an opaque structure holding the cuBLASLt library context. Use cublasLtCreate() to initialize the cuBLASLt library context and return a handle to an opaque structure holding the cuBLASLt library context, and use cublasLtDestroy() to destroy a previously created cuBLASLt library context descriptor and release the resources.
Note
cuBLAS handle (cublasHandle_t) encapsulates a cuBLASLt handle. Any valid cublasHandle_t can be used in place of cublasLtHandle_t with a simple cast. However, unlike a cuBLAS handle, a cuBLASLt handle is not tied to any particular CUDA context with the exception of CUDA contexts tied to a graphics context (starting from CUDA 12.8). If a cuBLASLt handle is created when the current CUDA context is tied to a graphics context, then cuBLASLt detects the corresponding shared memory limitations and records it in the handle.
3.3.4. cublasLtLoggerCallback_t
cublasLtLoggerCallback_t is a callback function pointer type. A callback function can be set using cublasLtLoggerSetCallback().
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
See cuBLASLt Logging. |
|
|
Output |
The name of the API that logged this message. |
|
|
Output |
The log message. |
3.3.5. cublasLtMatmulAlgo_t
cublasLtMatmulAlgo_t is an opaque structure holding the description of the matrix multiplication algorithm. This structure can be trivially serialized and later restored for use with the same version of cuBLAS library to save on selecting the right configuration again.
3.3.6. cublasLtMatmulAlgoCapAttributes_t
cublasLtMatmulAlgoCapAttributes_t enumerates matrix multiplication algorithm capability attributes that can be retrieved from an initialized cublasLtMatmulAlgo_t descriptor using cublasLtMatmulAlgoCapGetAttribute().
Value |
Description |
Data Type |
|---|---|---|
|
Support for split-K. Boolean (0 or 1) to express if split-K implementation is supported. 0 means no support, and supported otherwise. See |
|
|
Mask to express the types of reduction schemes supported, see cublasLtReductionScheme_t. If the reduction scheme is not masked out then it is supported. For example: |
|
|
Support for CTA-swizzling. Boolean (0 or 1) to express if CTA-swizzling implementation is supported. 0 means no support, and 1 means supported value of 1; other values are reserved. See also |
|
|
Support strided batch. 0 means no support, supported otherwise. |
|
|
Support pointer array batch. 0 means no support, supported otherwise. |
|
|
Experimental: Support pointer array grouped. 0 means no support, supported otherwise. See |
|
|
Support results out of place (D != C in D = alpha.A.B + beta.C). 0 means no support, supported otherwise. |
|
|
Syrk (symmetric rank k update)/herk (Hermitian rank k update) support (on top of regular gemm). 0 means no support, supported otherwise. |
|
|
The tile ids possible to use. See cublasLtMatmulTile_t. If no tile ids are supported then use |
|
|
The stages ids possible to use. See cublasLtMatmulStages_t. If no stages ids are supported then use |
|
|
Custom option range is from 0 to |
|
|
Indicates whether the algorithm is using regular compute or tensor operations. 0 means regular compute, 1 means tensor operations. DEPRECATED |
|
|
Indicate whether the algorithm implements the Gaussian optimization of complex matrix multiplication. 0 means regular compute; 1 means Gaussian. See cublasMath_t. DEPRECATED |
|
|
Indicates whether the algorithm supports custom (not COL or ROW memory order). 0 means only COL and ROW memory order is allowed, non-zero means that algo might have different requirements. See cublasLtOrder_t. |
|
|
Bitmask enumerating the pointer modes the algorithm supports. See cublasLtPointerModeMask_t. |
|
|
Bitmask enumerating the kinds of postprocessing algorithm supported in the epilogue. See cublasLtEpilogue_t. |
|
|
Support for negative leading dimension for all of the matrices. 0 means no support, supported otherwise. |
|
|
Details about algorithm’s implementation that affect it’s numerical behavior. See cublasLtNumericalImplFlags_t. |
|
|
Minimum alignment required for A matrix in bytes. |
|
|
Minimum alignment required for B matrix in bytes. |
|
|
Minimum alignment required for C matrix in bytes. |
|
|
Minimum alignment required for D matrix in bytes. |
|
|
Support for for floating point emulation. See Floating Point Emulation. |
|
3.3.7. cublasLtMatmulAlgoConfigAttributes_t
cublasLtMatmulAlgoConfigAttributes_t is an enumerated type that contains the configuration attributes for cuBLASLt matrix multiply algorithms. The configuration attributes are algorithm-specific, and can be set. The attributes configuration of a given algorithm should agree with its capability attributes. Use cublasLtMatmulAlgoConfigGetAttribute() and cublasLtMatmulAlgoConfigSetAttribute() to get and set the attribute value of a matmul algorithm descriptor.
Value |
Description |
Data Type |
|---|---|---|
|
Read-only attribute. Algorithm index. See cublasLtMatmulAlgoGetIds(). Set by cublasLtMatmulAlgoInit(). |
|
|
Tile id. See cublasLtMatmulTile_t. Default: |
|
|
stages id, see cublasLtMatmulStages_t. Default: |
|
|
Number of K splits. If the number of K splits is greater than one, SPLITK_NUM parts of matrix multiplication will be computed in parallel. The results will be accumulated according to |
|
|
Reduction scheme to use when splitK value > 1. Default: |
|
|
Enable/Disable CTA swizzling. Change mapping from CUDA grid coordinates to parts of the matrices. Possible values: 0 and 1; other values reserved. |
|
|
Custom option value. Each algorithm can support some custom options that don’t fit the description of the other configuration attributes. See the |
|
|
Inner shape ID. Refer to |
|
|
Cluster shape ID. Refer to |
|
3.3.8. cublasLtMatmulDesc_t
The cublasLtMatmulDesc_t is a pointer to an opaque structure holding the description of the matrix multiplication operation cublasLtMatmul(). A descriptor can be created by calling cublasLtMatmulDescCreate() and destroyed by calling cublasLtMatmulDescDestroy().
3.3.9. cublasLtMatmulDescAttributes_t
cublasLtMatmulDescAttributes_t is a descriptor structure containing the attributes that define the specifics of the matrix multiply operation. Use cublasLtMatmulDescGetAttribute() and cublasLtMatmulDescSetAttribute() to get and set the attribute value of a matmul descriptor.
Value |
Description |
Data Type |
|---|---|---|
|
Compute type. Defines the data type used for multiply and accumulate operations, and the accumulator during the matrix multiplication. See cublasComputeType_t. |
|
|
Scale type. Defines the data type of the scaling factors |
|
|
Specifies |
|
|
Specifies the type of transformation operation that should be performed on matrix A. Default value is: |
|
|
Specifies the type of transformation operation that should be performed on matrix B. Default value is: |
|
|
Specifies the type of transformation operation that should be performed on matrix C. Currently only |
|
|
Indicates whether the lower or upper part of the dense matrix was filled, and consequently should be used by the function. Currently this flag is not supported for bfloat16 or FP8 data types and is not supported on the following GPUs: Hopper, Blackwell. Default value is: |
|
|
Epilogue function. See cublasLtEpilogue_t. Default value is: |
|
|
Bias or Bias gradient vector pointer in the device memory.
Bias vector elements are the same type as |
|
|
Stride (in elements) to the next bias or bias gradient vector for strided batch operations. The default value is 0. |
|
|
Pointer for epilogue auxiliary buffer.
For aux data type, see |
|
|
Leading dimension for epilogue auxiliary buffer.
|
|
|
Batch stride for epilogue auxiliary buffer.
Default value: 0. |
|
|
Batch stride for alpha vector. Used together with |
|
|
Number of SMs to target for parallel execution. Optimizes heuristics for execution on a different number of SMs when user expects a concurrent stream to be using some of the device resources. Default value: 0. |
|
|
Device pointer to the scale factor value that converts data in matrix A to the compute data type range. The scaling factor must have the same type as the compute type. If not specified, or set to NULL, the scaling factor is assumed to be 1. If set for an unsupported matrix data, scale, and compute type combination, calling cublasLtMatmul() will return |
|
|
Equivalent to |
|
|
Equivalent to |
|
|
Equivalent to |
|
|
Device pointer to the memory location that on completion will be set to the maximum of absolute values in the output matrix. The computed value has the same type as the compute type. If not specified, or set to NULL, the maximum absolute value is not computed. If set for an unsupported matrix data, scale, and compute type combination, calling cublasLtMatmul() will return |
|
|
The type of the data that will be stored in
When CType is If set for an unsupported matrix data, scale, and compute type combination, calling cublasLtMatmul() will return |
|
|
Device pointer to the scaling factor value to convert results from compute type data range to storage data range in the auxiliary matrix that is set via |
|
|
Device pointer to the memory location that on completion will be set to the maximum of absolute values in the buffer that is set via |
|
|
Flag for managing FP8 fast accumulation mode. When enabled, on some GPUs problem execution might be faster but at the cost of lower accuracy because intermediate results will not periodically be promoted to a higher precision. Currently this flag has an effect on the following GPUs: Ada, Hopper. Default value: 0 - fast accumulation mode is disabled |
|
|
Type of the bias or bias gradient vector in the device memory. Bias case: see
Default value: -1 |
|
|
Scaling mode that defines how the matrix scaling factor for matrix A is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Scaling mode that defines how the matrix scaling factor for matrix B is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Scaling mode that defines how the matrix scaling factor for matrix C is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Scaling mode that defines how the matrix scaling factor for matrix D is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Scaling mode that defines how the matrix scaling factor for the auxiliary matrix is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Device pointer to the scale factors that are used to convert data in matrix D to the compute data type range. The scaling factor value type is defined by the scaling mode (see |
|
|
Scaling mode that defines how the output matrix scaling factor for matrix D is interpreted. Default value: 0. See cublasLtMatmulMatrixScale_t. |
|
|
Emulation descriptor to configure floating point emulation parameters. Default value: NULL. |
|
|
Experimental: Batch stride for alpha. Applicable when matrix D’s |
|
|
Experimental: Batch stride for beta. Applicable when matrix D’s |
|
3.3.10. cublasLtMatmulHeuristicResult_t
cublasLtMatmulHeuristicResult_t is a descriptor that holds the configured matrix multiplication algorithm descriptor and its runtime properties.
Member |
Description |
|---|---|
cublasLtMatmulAlgo_t algo |
Must be initialized with cublasLtMatmulAlgoInit() if the preference |
|
Actual size of workspace memory required. |
cublasStatus_t state; |
Result status. Other fields are valid only if, after call to cublasLtMatmulAlgoGetHeuristic(), this member is set to |
|
Waves count is a device utilization metric. A |
|
Reserved. |
3.3.11. cublasLtMatmulInnerShape_t
cublasLtMatmulInnerShape_t is an enumerated type used to configure various aspects of the internal kernel design. This does not impact the CUDA grid size.
Value |
Description |
|---|---|
|
Inner shape is undefined. |
|
Inner shape is MMA884. |
|
Inner shape is MMA1684. |
|
Inner shape is MMA1688. |
|
Inner shape is MMA16816. |
3.3.12. cublasLtMatmulPreference_t
The cublasLtMatmulPreference_t is a pointer to an opaque structure holding the description of the preferences for cublasLtMatmulAlgoGetHeuristic() configuration. Use cublasLtMatmulPreferenceCreate() to create one instance of the descriptor and cublasLtMatmulPreferenceDestroy() to destroy a previously created descriptor and release the resources.
3.3.13. cublasLtMatmulPreferenceAttributes_t
cublasLtMatmulPreferenceAttributes_t is an enumerated type used to apply algorithm search preferences while fine-tuning the heuristic function. Use cublasLtMatmulPreferenceGetAttribute() and cublasLtMatmulPreferenceSetAttribute() to get and set the attribute value of a matmul preference descriptor.
Value |
Description |
Data Type |
|---|---|---|
|
Search mode. See cublasLtMatmulSearch_t. Default is |
|
|
Maximum allowed workspace memory. Default is 0 (no workspace memory allowed). |
|
|
Reduction scheme mask. See cublasLtReductionScheme_t. Only algorithm configurations specifying |
|
|
Minimum buffer alignment for matrix A (in bytes). Selecting a smaller value will exclude algorithms that can not work with matrix A, which is not as strictly aligned as the algorithms need. Default is 256 bytes. |
|
|
Minimum buffer alignment for matrix B (in bytes). Selecting a smaller value will exclude algorithms that can not work with matrix B, which is not as strictly aligned as the algorithms need. Default is 256 bytes. |
|
|
Minimum buffer alignment for matrix C (in bytes). Selecting a smaller value will exclude algorithms that can not work with matrix C, which is not as strictly aligned as the algorithms need. Default is 256 bytes. |
|
|
Minimum buffer alignment for matrix D (in bytes). Selecting a smaller value will exclude algorithms that can not work with matrix D, which is not as strictly aligned as the algorithms need. Default is 256 bytes. |
|
|
Maximum wave count. See cublasLtMatmulHeuristicResult_t |
|
|
Numerical implementation details mask. See cublasLtNumericalImplFlags_t. Filters heuristic result to only include algorithms that use the allowed implementations. default: uint64_t(-1) (allow everything) |
|
|
Experimental: Average reduction dimension. This is only supported when all matrix descriptors have |
|
|
Experimental: Average rows of matrix D. This is only supported when all matrix descriptors have |
|
|
Experimental: Average columns of matrix D. This is only supported when all matrix descriptors have |
|
3.3.14. cublasLtMatmulSearch_t
cublasLtMatmulSearch_t is an enumerated type that contains the attributes for heuristics search type.
Value |
Description |
Data Type |
|---|---|---|
|
Request heuristics for the best algorithm for the given use case. |
|
|
Request heuristics only for the pre-configured algo id. |
3.3.15. cublasLtMatmulTile_t
cublasLtMatmulTile_t is an enumerated type used to set the tile size in rows x columns. See also CUTLASS: Fast Linear Algebra in CUDA C++.
Value |
Description |
|---|---|
|
Tile size is undefined. |
|
Tile size is 8 rows x 8 columns. |
|
Tile size is 8 rows x 16 columns. |
|
Tile size is 16 rows x 8 columns. |
|
Tile size is 8 rows x 32 columns. |
|
Tile size is 16 rows x 16 columns. |
|
Tile size is 32 rows x 8 columns. |
|
Tile size is 8 rows x 64 columns. |
|
Tile size is 16 rows x 32 columns. |
|
Tile size is 32 rows x 16 columns. |
|
Tile size is 64 rows x 8 columns. |
|
Tile size is 32 rows x 32 columns. |
|
Tile size is 32 rows x 64 columns. |
|
Tile size is 64 rows x 32 columns. |
|
Tile size is 32 rows x 128 columns. |
|
Tile size is 64 rows x 64 columns. |
|
Tile size is 128 rows x 32 columns. |
|
Tile size is 64 rows x 128 columns. |
|
Tile size is 128 rows x 64 columns. |
|
Tile size is 64 rows x 256 columns. |
|
Tile size is 128 rows x 128 columns. |
|
Tile size is 256 rows x 64 columns. |
|
Tile size is 64 rows x 512 columns. |
|
Tile size is 128 rows x 256 columns. |
|
Tile size is 256 rows x 128 columns. |
|
Tile size is 512 rows x 64 columns. |
|
Tile size is 64 rows x 96 columns. |
|
Tile size is 96 rows x 64 columns. |
|
Tile size is 96 rows x 128 columns. |
|
Tile size is 128 rows x 160 columns. |
|
Tile size is 160 rows x 128 columns. |
|
Tile size is 192 rows x 128 columns. |
|
Tile size is 128 rows x 192 columns. |
|
Tile size is 128 rows x 96 columns. |
3.3.16. cublasLtMatmulStages_t
cublasLtMatmulStages_t is an enumerated type used to configure the size and number of shared memory buffers where input elements are staged. Number of staging buffers defines kernel’s pipeline depth.
Value |
Description |
|---|---|
|
Stage size is undefined. |
|
Stage size is 16, number of stages is 1. |
|
Stage size is 16, number of stages is 2. |
|
Stage size is 16, number of stages is 3. |
|
Stage size is 16, number of stages is 4. |
|
Stage size is 16, number of stages is 5. |
|
Stage size is 16, number of stages is 6. |
|
Stage size is 32, number of stages is 1. |
|
Stage size is 32, number of stages is 2. |
|
Stage size is 32, number of stages is 3. |
|
Stage size is 32, number of stages is 4. |
|
Stage size is 32, number of stages is 5. |
|
Stage size is 32, number of stages is 6. |
|
Stage size is 64, number of stages is 1. |
|
Stage size is 64, number of stages is 2. |
|
Stage size is 64, number of stages is 3. |
|
Stage size is 64, number of stages is 4. |
|
Stage size is 64, number of stages is 5. |
|
Stage size is 64, number of stages is 6. |
|
Stage size is 128, number of stages is 1. |
|
Stage size is 128, number of stages is 2. |
|
Stage size is 128, number of stages is 3. |
|
Stage size is 128, number of stages is 4. |
|
Stage size is 128, number of stages is 5. |
|
Stage size is 128, number of stages is 6. |
|
Stage size is 32, number of stages is 10. |
|
Stage size is 8, number of stages is 4. |
|
Stage size is 16, number of stages is 10. |
|
Stage size is 8, number of stages is 5. |
|
Stage size is 8, number of stages is 3. |
|
Stage size is 8, number of stages is selected automatically. |
|
Stage size is 16, number of stages is selected automatically. |
|
Stage size is 32, number of stages is selected automatically. |
|
Stage size is 64, number of stages is selected automatically. |
|
Stage size is 128, number of stages is selected automatically. |
|
Stage size is 256, number of stages is selected automatically. |
|
Stage size is 768, number of stages is selected automatically. |
3.3.17. cublasLtNumericalImplFlags_t
cublasLtNumericalImplFlags_t: a set of bit-flags that can be specified to select implementation details that may affect numerical behavior of algorithms.
Flags below can be combined using the bit OR operator “|”.
Value |
Description |
|---|---|
|
Specify that the implementation is based on [H,F,D]FMA (fused multiply-add) family instructions. |
|
Specify that the implementation is based on HMMA (tensor operation) family instructions. |
|
Specify that the implementation is based on IMMA (integer tensor operation) family instructions. |
|
Specify that the implementation is based on DMMA (double precision tensor operation) family instructions. |
|
Mask to filter implementations using any of the above kinds of tensor operations. |
|
Mask to filter implementation details about multiply-accumulate instructions used. |
|
Specify that the implementation’s inner dot product is using half precision accumulator. |
|
Specify that the implementation’s inner dot product is using single precision accumulator. |
|
Specify that the implementation’s inner dot product is using double precision accumulator. |
|
Specify that the implementation’s inner dot product is using 32 bit signed integer precision accumulator. |
|
Mask to filter implementation details about accumulator used. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using half-precision inputs. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using bfloat16 inputs. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using TF32 inputs. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using single-precision inputs. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using double-precision inputs. |
|
Specify that the implementation’s inner dot product multiply-accumulate instruction is using 8-bit integer inputs. |
|
Mask to filter implementation details about accumulator input used. |
|
Specify that the implementation applies Gauss complexity reduction algorithm to reduce arithmetic complexity of the complex matrix multiplication problem |
3.3.18. cublasLtMatrixLayout_t
The cublasLtMatrixLayout_t is a pointer to an opaque structure holding the description of a matrix layout. Use cublasLtMatrixLayoutCreate() or cublasLtGroupedMatrixLayoutCreate() to create one instance of the descriptor and cublasLtMatrixLayoutDestroy() to destroy a previously created descriptor and release the resources.
3.3.19. cublasLtMatrixLayoutAttribute_t
cublasLtMatrixLayoutAttribute_t is a descriptor structure containing the attributes that define the details of the matrix operation. Use cublasLtMatrixLayoutGetAttribute() and cublasLtMatrixLayoutSetAttribute() to get and set the attribute value of a matrix layout descriptor.
Value |
Description |
Data Type |
|---|---|---|
|
Specifies the data precision type. See cudaDataType_t. |
|
|
Specifies the memory order of the data of the matrix. Default value is |
|
|
Describes the number of rows in the matrix. Normally only values that can be expressed as |
|
|
Describes the number of columns in the matrix. Normally only values that can be expressed as |
|
|
The leading dimension of the matrix. For
|
|
|
Number of matmul operations to perform in the batch. Default value is 1. See also |
|
|
Stride (in elements) to the next matrix for the strided batch operation. Default value is 0. When matrix type is planar-complex ( |
|
|
Stride (in bytes) to the imaginary plane for planar-complex layout. Default value is 0, indicating that the layout is regular (real and imaginary parts of complex numbers are interleaved in memory for each element). |
|
|
The batch mode of the matrix. Default value is |
|
|
Experimental: a device pointer to the array of rows in a grouped matrix. The length of the array must be equal to |
|
|
Experimental: a device pointer to the array of columns in a grouped matrix. The length of the array must be equal to |
|
|
Experimental: a device pointer to the array of leading dimensions in a grouped matrix. The length of the array must be equal to |
|
|
Experimental: cublasLtIntegerWidth_t is an enumerated type used to indicate the width of integers in the rows and columns arrays of a grouped matrix. Default value is |
|
|
Experimental: cublasLtIntegerWidth_t is an enumerated type used to indicate the width of integers in the leading dimensions array of a grouped matrix. Default value is |
|
3.3.20. cublasLtIntegerWidth_t
Experimental: cublasLtIntegerWidth_t is an enumerated type used to indicate the width of integers in the dimensions arrays of a grouped matrix.
Value |
Description |
|---|---|
|
32-bit integer width. |
|
64-bit integer width. |
3.3.21. cublasLtMatrixTransformDesc_t
The cublasLtMatrixTransformDesc_t is a pointer to an opaque structure holding the description of a matrix transformation operation. Use cublasLtMatrixTransformDescCreate() to create one instance of the descriptor and cublasLtMatrixTransformDescDestroy() to destroy a previously created descriptor and release the resources.
3.3.22. cublasLtMatrixTransformDescAttributes_t
cublasLtMatrixTransformDescAttributes_t is a descriptor structure containing the attributes that define the specifics of the matrix transform operation. Use cublasLtMatrixTransformDescGetAttribute() and cublasLtMatrixTransformDescSetAttribute() to set the attribute value of a matrix transform descriptor.
Value |
Description |
Data Type |
|---|---|---|
|
Scale type. Inputs are converted to the scale type for scaling and summation, and results are then converted to the output type to store in the memory. For the supported data types see cudaDataType_t. |
|
|
Specifies the scalars alpha and beta are passed by reference whether on the host or on the device. Default value is: |
|
|
Specifies the type of operation that should be performed on the matrix A. Default value is: |
|
|
Specifies the type of operation that should be performed on the matrix B. Default value is: |
|
3.3.23. cublasLtOrder_t
cublasLtOrder_t is an enumerated type used to indicate the data ordering of the matrix.
Value |
Description |
|---|---|
|
Data is ordered in column-major format. The leading dimension is the stride (in elements) to the beginning of next column in memory. |
|
Data is ordered in row-major format. The leading dimension is the stride (in elements) to the beginning of next row in memory. |
|
Data is ordered in column-major ordered tiles of 32 columns. The leading dimension is the stride (in elements) to the beginning of next group of 32-columns.
For example, if the matrix has 33 columns and 2 rows, then the leading dimension must be at least |
|
Data is ordered in column-major ordered tiles of composite tiles with total 32 columns and 8 rows. A tile is composed of interleaved inner tiles of 4 columns within 4 even or odd rows in an alternating pattern.
The leading dimension is the stride (in elements) to the beginning of the first 32 column x 8 row tile for the next 32-wide group of columns. For example, if the matrix has 33 columns and 1 row,
the leading dimension must be at least |
|
Data is ordered in column-major ordered tiles of composite tiles with total 32 columns ands 32 rows. Element offset within the tile is calculated as |
3.3.24. cublasLtPointerMode_t
cublasLtPointerMode_t is an enumerated type used to set the pointer mode for the scaling factors alpha and beta.
Value |
Description |
|---|---|
|
Matches |
|
Matches |
|
Pointers target device memory vectors of length equal to the number of rows of matrix D. |
|
|
|
|
Note
Only pointer modes CUBLASLT_POINTER_MODE_HOST and CUBLASLT_POINTER_MODE_DEVICE are supported when cublasLtBatchMode_t of any matrix is set to CUBLASLT_BATCH_MODE_POINTER_ARRAY or CUBLASLT_BATCH_MODE_GROUPED.
3.3.25. cublasLtPointerModeMask_t
cublasLtPointerModeMask_t is an enumerated type used to define and query the pointer mode capability.
Value |
Description |
|---|---|
|
See |
|
See |
|
See |
|
See |
|
See |
3.3.26. cublasLtReductionScheme_t
cublasLtReductionScheme_t is an enumerated type used to specify a reduction scheme for the portions of the dot-product calculated in parallel (i.e., “split - K”).
Value |
Description |
|---|---|
|
Do not apply reduction. The dot-product will be performed in one sequence. |
|
Reduction is performed “in place” using the output buffer, parts are added up in the output data type. Workspace is only used for counters that guarantee sequentiality. |
|
Reduction done out of place in a user-provided workspace. The intermediate results are stored in the compute type in the workspace and reduced in a separate step. |
|
Reduction done out of place in a user-provided workspace. The intermediate results are stored in the output type in the workspace and reduced in a separate step. |
|
Allows all reduction schemes. |
3.3.27. cublasLtMatmulMatrixScale_t
cublasLtMatmulMatrixScale_t is an enumerated type used to specify scaling mode that defines how scaling factor pointers are interpreted.
Value |
Description |
|---|---|
|
Scaling factors are single-precision scalars applied to the whole tensors (this mode is the default for fp8). This is the only value valid for |
|
Scaling factors are tensors that contain a dedicated scaling factor stored as an 8-bit |
|
Scaling factors are tensors that contain a dedicated scaling factor stored as an 8-bit |
|
Scaling factors are vectors of CUDA_R_32F values. This mode is only applicable to matrices A and B, in which case the vectors are expected to have M and N elements respectively, and each (i, j)-th element of product of A and B is multiplied by i-th element of A scale and j-th element of B scale. |
|
Scaling factors are tensors that contain a dedicated CUDA_R_32F scaling factor for each 128-element block in the innermost dimension of the corresponding data tensor. |
|
Scaling factors are tensors that contain a dedicated CUDA_R_32F scaling factor for each 128x128-element block in the the corresponding data tensor. |
3.3.28. cublasLtBatchMode_t
Value |
Description |
|---|---|
|
The matrices of each instance of the batch are located at fixed offsets in number of elements from their locations in the previous instance. |
|
The address of the matrix of each instance of the batch are read from device arrays of pointers. |
|
Experimental: The address of the matrix of each instance of the group are read from device arrays of pointers. Each group can have different columns, rows, and leading dimensions. See cublasLtMatrixLayout_t for more details. |
3.3.29. cublasLtEmulationDesc_t
cublasLtEmulationDesc_t is a pointer to an opaque structure holding the emulation descriptor. Use cublasLtEmulationDescCreate() to create a new emulation descriptor, and cublasLtEmulationDescDestroy() to destroy it and release the resources.
3.3.30. cublasLtEmulationDescAttributes_t
cublasLtEmulationDescAttributes_t is an enumerated type used to configure floating point emulation parameters. See Floating Point Emulation documentation for more details.
Value |
Description |
Data Type |
|---|---|---|
|
Strategy, see cublasEmulationStrategy_t. Defines when to use floating point emulation algorithms. Default: EMULATION_STRATEGY_DEFAULT. |
|
|
Special values support, see cudaEmulationSpecialValuesSupport_t. Defines a bit mask of special cases in floating-point representations that must be supported. Default: EMULATION_SPECIAL_VALUES_SUPPORT_DEFAULT. |
|
|
Mantissa control, see cudaEmulationMantissaControl_t. For fixed-point emulation, defines how to compute the number of retained mantissa bits. See Floating Point Emulation documentation for more details. |
|
|
For fixed-point emulation only. An int32_t representing the maximum (up to quantization) number of mantissa bits to retain during fixed-point emulation. A default value of 0 allows the library to select a reasonable value based on device properties. Default: 0. |
|
|
This parameter is for fixed-point emulation with |
|
|
This parameter is for fixed-point emulation. A device pointer which will contain the number of mantissa bits that were retained. If emulation is not used, the pointer will contain -1. Default: nullptr. |
|
3.4. cuBLASLt API Reference
3.4.1. cublasLtCreate()
cublasStatus_t
cublasLtCreate(cublasLtHandle_t *lighthandle)
This function initializes the cuBLASLt library and creates a handle to an opaque structure holding the cuBLASLt library context. It allocates light hardware resources on the host and device, and must be called prior to making any other cuBLASLt library calls.
The cuBLASLt library context is tied to the current CUDA device. To use the library on multiple devices, one cuBLASLt handle must be created for each device. Furthermore, the device must be set as the current before invoking cuBLASLt functions with a handle tied to that device.
See also: cuBLAS Context.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the allocated cuBLASLt handle for the created cuBLASLt context. |
Returns:
Return Value |
Description |
|---|---|
|
The allocation completed successfully. |
|
The cuBLASLt library was not initialized. This usually happens:
|
|
Resource allocation failed inside the cuBLASLt library. This is usually caused by a To correct: prior to the function call, deallocate the previously allocated memory as much as possible. |
|
|
See cublasStatus_t for a complete list of valid return codes.
3.4.2. cublasLtDestroy()
cublasStatus_t
cublasLtDestroy(cublasLtHandle_t lightHandle)
This function releases hardware resources used by the cuBLASLt library. This function is usually the last call with a particular handle to the cuBLASLt library. Because cublasLtCreate() allocates some internal resources and the release of those resources by calling cublasLtDestroy() will implicitly call cudaDeviceSynchronize(), it is recommended to minimize the number of times these functions are called.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the cuBLASLt handle to be destroyed. |
Returns:
Return Value |
Meaning |
|---|---|
|
The cuBLASLt context was successfully destroyed. |
|
The cuBLASLt library was not initialized. |
|
|
See cublasStatus_t for a complete list of valid return codes.
3.4.3. cublasLtDisableCpuInstructionsSetMask()
unsigned cublasLtDisableCpuInstructionsSetMask(unsigned mask);
Instructs cuBLASLt library to not use CPU instructions specified by the flags in the mask.
The function takes precedence over the CUBLASLT_DISABLE_CPU_INSTRUCTIONS_MASK environment variable.
Parameters: mask – the flags combined with bitwise OR(|) operator that specify which CPU instructions should not be used.
Supported flags:
Value |
Description |
|---|---|
|
x86-64 AVX512 ISA. |
Returns: the previous value of the mask.
3.4.4. cublasLtGetCudartVersion()
size_t cublasLtGetCudartVersion(void);
This function returns the version number of the CUDA Runtime library.
Parameters: None.
Returns:size_t - The version number of the CUDA Runtime library.
3.4.5. cublasLtGetProperty()
cublasStatus_t cublasLtGetProperty(libraryPropertyType type, int *value);
This function returns the value of the requested property by writing it to the memory location pointed to by the value parameter.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Of the type |
|
|
Output |
Pointer to the host memory location where the requested information should be written. |
Returns:
Return Value |
Meaning |
|---|---|
|
The requested |
|
|
See cublasStatus_t for a complete list of valid return codes.
3.4.6. cublasLtGetStatusName()
const char* cublasLtGetStatusName(cublasStatus_t status);
Returns the string representation of a given status.
Parameters: cublasStatus_t - the status.
Returns: const char* - the NULL-terminated string.
3.4.7. cublasLtGetStatusString()
const char* cublasLtGetStatusString(cublasStatus_t status);
Returns the description string for a given status.
Parameters: cublasStatus_t - the status.
Returns: const char* - the NULL-terminated string.
3.4.8. cublasLtHeuristicsCacheGetCapacity()
cublasStatus_t cublasLtHeuristicsCacheGetCapacity(size_t* capacity);
Returns the Heuristics Cache capacity.
Parameters:
Parameter |
Description |
|---|---|
|
The pointer to the returned capacity value. |
Returns:
Return Value |
Description |
|---|---|
|
The capacity was successfully written. |
|
The capacity was successfully set. |
3.4.9. cublasLtHeuristicsCacheSetCapacity()
cublasStatus_t cublasLtHeuristicsCacheSetCapacity(size_t capacity);
Sets the Heuristics Cache capacity. Set the capacity to 0 to disable the heuristics cache.
This function takes precedence over CUBLASLT_HEURISTICS_CACHE_CAPACITY environment variable.
Parameters:
Parameter |
Description |
|---|---|
|
The desirable heuristics cache capacity. |
Returns:
Return Value |
Description |
|---|---|
|
The capacity was successfully set. |
3.4.10. cublasLtGetVersion()
size_t cublasLtGetVersion(void);
This function returns the version number of cuBLASLt library.
Parameters: None.
Returns:size_t - The version number of cuBLASLt library.
3.4.11. cublasLtLoggerSetCallback()
cublasStatus_t cublasLtLoggerSetCallback(cublasLtLoggerCallback_t callback);
Experimental: This function sets the logging callback function.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to a callback function. See cublasLtLoggerCallback_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the callback function was successfully set. |
See cublasStatus_t for a complete list of valid return codes.
3.4.12. cublasLtLoggerSetFile()
cublasStatus_t cublasLtLoggerSetFile(FILE* file);
Experimental: This function sets the logging output file. Note: once registered using this function call, the provided file handle must not be closed unless the function is called again to switch to a different file handle.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to an open file. File should have write permission. |
Returns:
Return Value |
Description |
|---|---|
|
If logging file was successfully set. |
See cublasStatus_t for a complete list of valid return codes.
3.4.13. cublasLtLoggerOpenFile()
cublasStatus_t cublasLtLoggerOpenFile(const char* logFile);
Experimental: This function opens and sets the logging output file in the given path.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Path of the logging output file. |
Returns:
Return Value |
Description |
|---|---|
|
If the logging file was successfully opened. |
See cublasStatus_t for a complete list of valid return codes.
3.4.14. cublasLtLoggerSetLevel()
cublasStatus_t cublasLtLoggerSetLevel(int level);
Experimental: This function sets the value of the logging level.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Value of the logging level. See cuBLASLt Logging. |
Returns:
Return Value |
Description |
|---|---|
|
If the value was not a valid logging level. See cuBLASLt Logging. |
|
If the logging level was successfully set. |
See cublasStatus_t for a complete list of valid return codes.
3.4.15. cublasLtLoggerSetMask()
cublasStatus_t cublasLtLoggerSetMask(int mask);
Experimental: This function sets the value of the logging mask.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Value of the logging mask. See cuBLASLt Logging. |
Returns:
Return Value |
Description |
|---|---|
|
If the logging mask was successfully set. |
See cublasStatus_t for a complete list of valid return codes.
3.4.16. cublasLtLoggerForceDisable()
cublasStatus_t cublasLtLoggerForceDisable();
Experimental: This function disables logging for the entire run.
Returns:
Return Value |
Description |
|---|---|
|
If logging was successfully disabled. |
See cublasStatus_t for a complete list of valid return codes.
3.4.17. cublasLtMatmul()
cublasStatus_t cublasLtMatmul(
cublasLtHandle_t lightHandle,
cublasLtMatmulDesc_t computeDesc,
const void *alpha,
const void *A,
cublasLtMatrixLayout_t Adesc,
const void *B,
cublasLtMatrixLayout_t Bdesc,
const void *beta,
const void *C,
cublasLtMatrixLayout_t Cdesc,
void *D,
cublasLtMatrixLayout_t Ddesc,
const cublasLtMatmulAlgo_t *algo,
void *workspace,
size_t workspaceSizeInBytes,
cudaStream_t stream);
This function computes the matrix multiplication of matrices A and B to produce the output matrix D, according to the following operation:
D = alpha*(A*B) + beta*(C),
where A, B, and C are input matrices, and alpha and beta are input scalars.
Note
This function supports both in-place matrix multiplication (C == D and Cdesc == Ddesc) and out-of-place matrix multiplication (C != D, both matrices must have the same data type, number of rows, number of columns, batch size, and memory order). In the out-of-place case, the leading dimension of C can be different from the leading dimension of D. Specifically the leading dimension of C can be 0 to achieve row or column broadcast. If Cdesc is omitted, this function assumes it to be equal to Ddesc.
The workspace pointer must be aligned to at least a multiple of 256 bytes.
The recommendations on workspaceSizeInBytes are the same as mentioned in the cublasSetWorkspace() section.
Datatypes Supported:
cublasLtMatmul() supports the following computeType, scaleType, Atype/Btype, and Ctype. Footnotes can be found at the end of this section.
computeType |
scaleType |
Atype/Btype |
Ctype |
Bias Type 6 |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
Epilogue is not supported. |
|
|
|
Epilogue is not supported. |
|
|
|
|
|
|
|
|
|
|
||
|
|
Epilogue is not supported. |
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
Epilogue is not supported. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Epilogue is not supported. |
|
|
|
|
|
|
|
|
|
|
Epilogue is not supported. |
To use IMMA kernels, one of the following sets of requirements, with the first being the preferred one, must be met:
-
Using a regular data ordering:
All matrix pointers must be 4-byte aligned. For even better performance, this condition should hold with 16 instead of 4.
Leading dimensions of matrices A, B, C must be multiples of 4.
Only the “TN” format is supported - A must be transposed and B non-transposed.
Pointer mode can be
CUBLASLT_POINTER_MODE_HOST,CUBLASLT_POINTER_MODE_DEVICEorCUBLASLT_POINTER_MODE_ALPHA_DEVICE_VECTOR_BETA_HOST. With the latter mode, the kernels support theCUBLASLT_MATMUL_DESC_ALPHA_VECTOR_BATCH_STRIDEattribute.Dimensions m and k must be multiples of 4.
-
Using the IMMA-specific data ordering on Ampere (compute capability 8.0) or Turing (compute capability 7.5) (but not Hopper, compute capability 9.0, or later) architecture -
CUBLASLT_ORDER_COL32`for matrices A, C, D, and CUBLASLT_ORDER_COL4_4R2_8C (on Turing or Ampere architecture) orCUBLASLT_ORDER_COL32_2R_4R4(on Ampere architecture) for matrix B:Leading dimensions of matrices A, B, C must fulfill conditions specific to the memory ordering (see cublasLtOrder_t).
Matmul descriptor must specify
CUBLAS_OP_Ton matrix B andCUBLAS_OP_N(default) on matrix A and C.If scaleType
CUDA_R_32Iis used, the only supported values foralphaandbetaare0or1.Pointer mode can be
CUBLASLT_POINTER_MODE_HOST,CUBLASLT_POINTER_MODE_DEVICE,CUBLASLT_POINTER_MODE_DEVICE_VECTORorCUBLASLT_POINTER_MODE_ALPHA_DEVICE_VECTOR_BETA_ZERO. These kernels do not supportCUBLASLT_MATMUL_DESC_ALPHA_VECTOR_BATCH_STRIDE.Only the “NT” format is supported - A must be non-transposed and B transposed.
computeType |
scaleType |
Atype/Btype |
Ctype |
Bias Type |
|---|---|---|---|---|
|
|
|
|
|
Non-default epilogue not supported. |
|
|
|
CUDA_R_32F |
To use tensor- or block-scaled FP8 kernels, the following set of requirements must be satisfied:
All matrix dimensions must meet the optimal requirements listed in Tensor Core Usage (i.e. pointers and matrix dimension must support 16-byte alignment).
Scaling mode must meet the restrictions noted in the Scaling Mode Support Overview table.
A must be transposed and B non-transposed (The “TN” format) on Ada (compute capability 8.9), Hopper (compute capability 9.0), and Blackwell GeForce (compute capability 12.x) GPUs.
The compute type must be
CUBLAS_COMPUTE_32F.The scale type must be
CUDA_R_32F.
See the table below when using FP8 kernels:
AType |
BType |
CType |
DType |
Bias Type |
|---|---|---|---|---|
|
|
|
|
|
|
|
|||
|
|
|
||
|
|
|||
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|||
|
|
|
||
|
|
|||
|
|
|||
|
|
|
To use block-scaled FP4 kernels, the following set of requirements must be satisfied:
All matrix dimensions must meet the optimal requirements listed in Tensor Core Usage (i.e. pointers and matrix dimension must support 16-byte alignment).
Scaling mode must be
CUBLASLT_MATMUL_MATRIX_SCALE_VEC16_UE4M3A must be transposed and B non-transposed (The “TN” format)
The compute type must be
CUBLAS_COMPUTE_32F.The scale type must be
CUDA_R_32F.
AType |
BType |
CType |
DType |
Bias Type |
|---|---|---|---|---|
|
|
|
|
|
|
|
|||
|
|
|
||
|
|
|||
|
|
|
When A,B,C,D are planar-complex matrices (CUBLASLT_MATRIX_LAYOUT_PLANE_OFFSET != 0, see cublasLtMatrixLayoutAttribute_t) to make use of mixed precision tensor core acceleration, the following set of requirements must be satisfied:
computeType |
scaleType |
Atype/Btype |
Ctype |
|---|---|---|---|
|
|
|
|
|
|||
|
|
||
|
Experimental: To use cublasLtMatmul() with grouped matrices, the following set of requirements must be satisfied:
All matrix dimensions must meet the optimal requirements listed in Tensor Core Usage (i.e. pointers and matrix dimension must support 16-byte alignment).
GPU with one of the following compute capabilities: 10.x, 11.0.
The batch mode of all matrices must be
CUBLASLT_BATCH_MODE_GROUPED.The order type of all matrices must be
CUBLASLT_ORDER_COL.The scale mode of matrices
A,Bmust beCUBLASLT_MATMUL_MATRIX_SCALE_SCALAR_32ForCUBLASLT_MATMUL_MATRIX_SCALE_PER_BATCH_SCALAR_32F(for FP8 tensors).The scale mode of matrices
CandDmust beCUBLASLT_MATMUL_MATRIX_SCALE_SCALAR_32F.The epilogue must be
CUBLASLT_EPILOGUE_DEFAULT.The pointer mode must be
CUBLASLT_POINTER_MODE_HOSTorCUBLASLT_POINTER_MODE_DEVICE.
AType |
BType |
CType |
DType |
|---|---|---|---|
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
Note
Because the shape information for the matrices is only available on the GPU (see CUBLASLT_GROUPED_MATRIX_LAYOUT_ROWS_ARRAY, CUBLASLT_GROUPED_MATRIX_LAYOUT_COLS_ARRAY, and CUBLASLT_GROUPED_MATRIX_LAYOUT_LD_ARRAY), the arguments validation is very limited. So it is possible that invalid arguments are not detected which will result in an undefined behavior.
NOTES:
- 6(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33)
-
ReLU, dReLu, GELU, dGELU and Bias epilogue modes (see
CUBLASLT_MATMUL_DESC_EPILOGUEin cublasLtMatmulDescAttributes_t) are not supported when D matrix memory order is defined asCUBLASLT_ORDER_ROW. For best performance when using the bias vector, specify zero beta and set pointer mode toCUBLASLT_POINTER_MODE_HOST. - 7(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17)
-
Use of
CUBLAS_ORDER_ROWtogether withCUBLAS_OP_C(Hermitian operator) is not supported unless all of A, B, C, and D matrices use theCUBLAS_ORDER_ROWordering. - 8(1,2,3,4,5,6,7,8,9,10)
-
FP8 DType is not supported when scaling modes are one of
CUBLASLT_MATMUL_MATRIX_SCALE_OUTER_VEC_32F,CUBLASLT_MATMUL_MATRIX_SCALE_VEC128_32F, andCUBLASLT_MATMUL_MATRIX_SCALE_BLK128x128_32F.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Input |
Handle to a previously created matrix multiplication descriptor of type cublasLtMatmulDesc_t. |
|
|
Device or host |
Input |
Pointers to the scalars used in the multiplication. |
|
Device |
Input |
Pointers to the GPU memory associated with the corresponding descriptors |
|
Input |
Handles to the previous created descriptors of the type cublasLtMatrixLayout_t. |
|
|
Device |
Output |
Pointer to the GPU memory associated with the descriptor |
|
Input |
Handle to the previous created descriptor of the type cublasLtMatrixLayout_t. |
|
|
Input |
Handle for matrix multiplication algorithm to be used. See cublasLtMatmulAlgo_t. When NULL, an implicit heuristics query with default search preferences will be performed to determine actual algorithm to use. |
|
|
Device |
Pointer to the workspace buffer allocated in the GPU memory. Must be 256B aligned (i.e. lowest 8 bits of address must be 0). |
|
|
Input |
Size of the workspace. |
|
|
Host |
Input |
The CUDA stream where all the GPU work will be submitted. |
Returns:
Return Value |
Description |
|---|---|
|
If cuBLASLt handle has not been initialized. |
|
If the parameters are unexpectedly NULL, in conflict or in an impossible configuration. For example, when |
|
If the current implementation on the selected device doesn’t support the configured operation. |
|
If the configured operation cannot be run using the selected device. |
|
If CUDA reported an execution error from the device. |
|
If the operation completed successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.18. cublasLtMatmulAlgoCapGetAttribute()
cublasStatus_t cublasLtMatmulAlgoCapGetAttribute(
const cublasLtMatmulAlgo_t *algo,
cublasLtMatmulAlgoCapAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried capability attribute for an initialized cublasLtMatmulAlgo_t descriptor structure. The capability attribute value is retrieved from the enumerated type cublasLtMatmulAlgoCapAttributes_t.
For example, to get list of supported Tile IDs:
cublasLtMatmulTile_t tiles[CUBLASLT_MATMUL_TILE_END];
size_t num_tiles, size_written;
if (cublasLtMatmulAlgoCapGetAttribute(algo, CUBLASLT_ALGO_CAP_TILE_IDS, tiles, sizeof(tiles), &size_written) == CUBLAS_STATUS_SUCCESS) {
num_tiles = size_written / sizeof(tiles[0]);}
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created opaque structure holding the matrix multiply algorithm descriptor. See cublasLtMatmulAlgo_t. |
|
|
Input |
The capability attribute whose value will be retrieved by this function. See cublasLtMatmulAlgoCapAttributes_t. |
|
|
Output |
The attribute value returned by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.19. cublasLtMatmulAlgoCheck()
cublasStatus_t cublasLtMatmulAlgoCheck(
cublasLtHandle_t lightHandle,
cublasLtMatmulDesc_t operationDesc,
cublasLtMatrixLayout_t Adesc,
cublasLtMatrixLayout_t Bdesc,
cublasLtMatrixLayout_t Cdesc,
cublasLtMatrixLayout_t Ddesc,
const cublasLtMatmulAlgo_t *algo,
cublasLtMatmulHeuristicResult_t *result);
This function performs the correctness check on the matrix multiply algorithm descriptor for the matrix multiply operation cublasLtMatmul() function with the given input matrices A, B and C, and the output matrix D. It checks whether the descriptor is supported on the current device, and returns the result containing the required workspace and the calculated wave count.
Note
CUBLAS_STATUS_SUCCESS doesn’t fully guarantee that the algo will run. The algo will fail if, for example, the buffers are not correctly aligned. However, if cublasLtMatmulAlgoCheck() fails, the algo will not run.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Input |
Handle to a previously created matrix multiplication descriptor of type cublasLtMatmulDesc_t. |
|
|
Input |
Handles to the previously created matrix layout descriptors of the type cublasLtMatrixLayout_t. |
|
|
Input |
Descriptor which specifies which matrix multiplication algorithm should be used. See cublasLtMatmulAlgo_t. May point to |
|
|
Output |
Pointer to the structure holding the results returned by this function. The results comprise of the required workspace and the calculated wave count. The |
Returns:
Return Value |
Description |
|---|---|
|
If matrix layout descriptors or the operation descriptor do not match the |
|
If the |
|
If the |
|
If the check was successful. |
See cublasStatus_t for a complete list of valid return codes.
3.4.20. cublasLtMatmulAlgoConfigGetAttribute()
cublasStatus_t cublasLtMatmulAlgoConfigGetAttribute(
const cublasLtMatmulAlgo_t *algo,
cublasLtMatmulAlgoConfigAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried configuration attribute for an initialized cublasLtMatmulAlgo_t descriptor. The configuration attribute value is retrieved from the enumerated type cublasLtMatmulAlgoConfigAttributes_t.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created opaque structure holding the matrix multiply algorithm descriptor. See cublasLtMatmulAlgo_t. |
|
|
Input |
The configuration attribute whose value will be retrieved by this function. See cublasLtMatmulAlgoConfigAttributes_t. |
|
|
Output |
The attribute value returned by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.21. cublasLtMatmulAlgoConfigSetAttribute()
cublasStatus_t cublasLtMatmulAlgoConfigSetAttribute(
cublasLtMatmulAlgo_t *algo,
cublasLtMatmulAlgoConfigAttributes_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified configuration attribute for an initialized cublasLtMatmulAlgo_t descriptor. The configuration attribute is an enumerant of the type cublasLtMatmulAlgoConfigAttributes_t.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created opaque structure holding the matrix multiply algorithm descriptor. See cublasLtMatmulAlgo_t. |
|
|
Input |
The configuration attribute whose value will be set by this function. See cublasLtMatmulAlgoConfigAttributes_t. |
|
|
Input |
The value to which the configuration attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If the attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.22. cublasLtMatmulAlgoGetHeuristic()
cublasStatus_t cublasLtMatmulAlgoGetHeuristic(
cublasLtHandle_t lightHandle,
cublasLtMatmulDesc_t operationDesc,
cublasLtMatrixLayout_t Adesc,
cublasLtMatrixLayout_t Bdesc,
cublasLtMatrixLayout_t Cdesc,
cublasLtMatrixLayout_t Ddesc,
cublasLtMatmulPreference_t preference,
int requestedAlgoCount,
cublasLtMatmulHeuristicResult_t heuristicResultsArray[],
int *returnAlgoCount);
This function retrieves the possible algorithms for the matrix multiply operation cublasLtMatmul() function with the given input matrices A, B and C, and the output matrix D. The output is placed in heuristicResultsArray[] in the order of increasing estimated compute time.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Input |
Handle to a previously created matrix multiplication descriptor of type cublasLtMatmulDesc_t. |
|
|
Input |
Handles to the previously created matrix layout descriptors of the type cublasLtMatrixLayout_t. |
|
|
Input |
Pointer to the structure holding the heuristic search preferences descriptor. See cublasLtMatmulPreference_t. |
|
|
Input |
Size of the |
|
|
Output |
Array containing the algorithm heuristics and associated runtime characteristics, returned by this function, in the order of increasing estimated compute time. |
|
|
Output |
Number of algorithms returned by this function. This is the number of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If no heuristic function available for current configuration. |
|
If query was successful. Inspect |
See cublasStatus_t for a complete list of valid return codes.
Note
This function may load some kernels using CUDA Driver API which may fail when there is no available GPU memory. Do not allocate the entire VRAM before running cublasLtMatmulAlgoGetHeuristic().
3.4.23. cublasLtMatmulAlgoGetIds()
cublasStatus_t cublasLtMatmulAlgoGetIds(
cublasLtHandle_t lightHandle,
cublasComputeType_t computeType,
cudaDataType_t scaleType,
cudaDataType_t Atype,
cudaDataType_t Btype,
cudaDataType_t Ctype,
cudaDataType_t Dtype,
int requestedAlgoCount,
int algoIdsArray[],
int *returnAlgoCount);
This function retrieves the IDs of all the matrix multiply algorithms that are valid, and can potentially be run by the cublasLtMatmul() function, for given types of the input matrices A, B and C, and of the output matrix D.
Note
The IDs are returned in no particular order. To make sure the best possible algo is contained in the list, make requestedAlgoCount large enough to receive the full list. The list is guaranteed to be full if returnAlgoCount < requestedAlgoCount.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
lightHandle |
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Inputs |
Data types of the computation type, scaling factors and of the operand matrices. See cudaDataType_t. |
|
|
Input |
Number of algorithms requested. Must be > 0. |
|
|
Output |
Array containing the algorithm IDs returned by this function. |
|
|
Output |
Number of algorithms actually returned by this function. |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If query was successful. Inspect |
See cublasStatus_t for a complete list of valid return codes.
3.4.24. cublasLtMatmulAlgoInit()
cublasStatus_t cublasLtMatmulAlgoInit(
cublasLtHandle_t lightHandle,
cublasComputeType_t computeType,
cudaDataType_t scaleType,
cudaDataType_t Atype,
cudaDataType_t Btype,
cudaDataType_t Ctype,
cudaDataType_t Dtype,
int algoId,
cublasLtMatmulAlgo_t *algo);
This function initializes the matrix multiply algorithm structure for the cublasLtMatmul() , for a specified matrix multiply algorithm and input matrices A, B and C, and the output matrix D.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Input |
Compute type. See |
|
|
Input |
Scale type. See |
|
|
Input |
Datatype precision for the input and output matrices. See cudaDataType_t . |
|
|
Input |
Specifies the algorithm being initialized. Should be a valid |
|
|
Input |
Pointer to the opaque structure to be initialized. See cublasLtMatmulAlgo_t. |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If |
|
If the structure was successfully initialized. |
See cublasStatus_t for a complete list of valid return codes.
3.4.25. cublasLtMatmulDescCreate()
cublasStatus_t cublasLtMatmulDescCreate( cublasLtMatmulDesc_t *matmulDesc,
cublasComputeType_t computeType,
cudaDataType_t scaleType);
This function creates a matrix multiply descriptor by allocating the memory needed to hold its opaque structure.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix multiply descriptor created by this function. See cublasLtMatmulDesc_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix multiply descriptor this function creates. See cublasComputeType_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix transform descriptor this function creates. See cudaDataType_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.26. cublasLtMatmulDescInit()
cublasStatus_t cublasLtMatmulDescInit( cublasLtMatmulDesc_t matmulDesc,
cublasComputeType_t computeType,
cudaDataType_t scaleType);
This function initializes a matrix multiply descriptor in a previously allocated one.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix multiply descriptor initialized by this function. See cublasLtMatmulDesc_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix multiply descriptor this function initializes. See cublasComputeType_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix transform descriptor this function initializes. See cudaDataType_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.27. cublasLtMatmulDescDestroy()
cublasStatus_t cublasLtMatmulDescDestroy(
cublasLtMatmulDesc_t matmulDesc);
This function destroys a previously created matrix multiply descriptor object.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the structure holding the matrix multiply descriptor that should be destroyed by this function. See cublasLtMatmulDesc_t. |
Returns:
Return Value |
Description |
|---|---|
|
If operation was successful. |
See cublasStatus_t for a complete list of valid return codes.
3.4.28. cublasLtMatmulDescGetAttribute()
cublasStatus_t cublasLtMatmulDescGetAttribute(
cublasLtMatmulDesc_t matmulDesc,
cublasLtMatmulDescAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried attribute belonging to a previously created matrix multiply descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix multiply descriptor queried by this function. See cublasLtMatmulDesc_t. |
|
|
Input |
The attribute that will be retrieved by this function. See cublasLtMatmulDescAttributes_t. |
|
|
Output |
Memory address containing the attribute value retrieved by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.29. cublasLtMatmulDescSetAttribute()
cublasStatus_t cublasLtMatmulDescSetAttribute(
cublasLtMatmulDesc_t matmulDesc,
cublasLtMatmulDescAttributes_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified attribute belonging to a previously created matrix multiply descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix multiply descriptor queried by this function. See cublasLtMatmulDesc_t. |
|
|
Input |
The attribute that will be set by this function. See cublasLtMatmulDescAttributes_t. |
|
|
Input |
The value to which the specified attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If the attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.30. cublasLtMatmulPreferenceCreate()
cublasStatus_t cublasLtMatmulPreferenceCreate(
cublasLtMatmulPreference_t *pref);
This function creates a matrix multiply heuristic search preferences descriptor by allocating the memory needed to hold its opaque structure.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix multiply preferences descriptor created by this function. See cublasLtMatrixLayout_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.31. cublasLtMatmulPreferenceInit()
cublasStatus_t cublasLtMatmulPreferenceInit(
cublasLtMatmulPreference_t pref);
This function initializes a matrix multiply heuristic search preferences descriptor in a previously allocated one.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix multiply preferences descriptor created by this function. See cublasLtMatrixLayout_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.32. cublasLtMatmulPreferenceDestroy()
cublasStatus_t cublasLtMatmulPreferenceDestroy(
cublasLtMatmulPreference_t pref);
This function destroys a previously created matrix multiply preferences descriptor object.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the structure holding the matrix multiply preferences descriptor that should be destroyed by this function. See cublasLtMatmulPreference_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the operation was successful. |
See cublasStatus_t for a complete list of valid return codes.
3.4.33. cublasLtMatmulPreferenceGetAttribute()
cublasStatus_t cublasLtMatmulPreferenceGetAttribute(
cublasLtMatmulPreference_t pref,
cublasLtMatmulPreferenceAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried attribute belonging to a previously created matrix multiply heuristic search preferences descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix multiply heuristic search preferences descriptor queried by this function. See cublasLtMatmulPreference_t. |
|
|
Input |
The attribute that will be queried by this function. See cublasLtMatmulPreferenceAttributes_t. |
|
|
Output |
Memory address containing the attribute value retrieved by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.34. cublasLtMatmulPreferenceSetAttribute()
cublasStatus_t cublasLtMatmulPreferenceSetAttribute(
cublasLtMatmulPreference_t pref,
cublasLtMatmulPreferenceAttributes_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified attribute belonging to a previously created matrix multiply preferences descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix multiply preferences descriptor queried by this function. See cublasLtMatmulPreference_t. |
|
|
Input |
The attribute that will be set by this function. See cublasLtMatmulPreferenceAttributes_t. |
|
|
Input |
The value to which the specified attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If buf is NULL or |
|
If the attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.35. cublasLtMatrixLayoutCreate()
cublasStatus_t cublasLtMatrixLayoutCreate( cublasLtMatrixLayout_t *matLayout,
cudaDataType type,
uint64_t rows,
uint64_t cols,
int64_t ld);
This function creates a matrix layout descriptor by allocating the memory needed to hold its opaque structure.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix layout descriptor created by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix layout descriptor this function creates. See cudaDataType_t. |
|
|
Input |
Number of rows and columns of the matrix. |
|
|
Input |
The leading dimension of the matrix. In column major layout, this is the number of elements to jump to reach the next column. Thus |
Returns:
Return Value |
Description |
|---|---|
|
If the memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.36. cublasLtMatrixLayoutInit()
cublasStatus_t cublasLtMatrixLayoutInit( cublasLtMatrixLayout_t matLayout,
cudaDataType type,
uint64_t rows,
uint64_t cols,
int64_t ld);
This function initializes a matrix layout descriptor in a previously allocated one.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix layout descriptor initialized by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix layout descriptor this function initializes. See cudaDataType_t. |
|
|
Input |
Number of rows and columns of the matrix. |
|
|
Input |
The leading dimension of the matrix. In column major layout, this is the number of elements to jump to reach the next column. Thus |
Returns:
Return Value |
Description |
|---|---|
|
If the memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.37. cublasLtGroupedMatrixLayoutCreate()
cublasStatus_t cublasLtGroupedMatrixLayoutCreate( cublasLtMatrixLayout_t *matLayout,
cudaDataType type,
int groupCount,
const void* rows_array,
const void* cols_array,
const void* ld_array);
Experimental: This function creates a grouped matrix layout descriptor by allocating the memory needed to hold its opaque structure.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix layout descriptor created by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix layout descriptor this function creates. See cudaDataType_t. |
|
|
Input |
Number of groups in the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of rows of the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of columns of the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of leading dimensions of the grouped matrix layout descriptor. |
Returns:
Return Value |
Description |
|---|---|
|
If the memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.38. cublasLtGroupedMatrixLayoutInit()
cublasStatus_t cublasLtGroupedMatrixLayoutInit( cublasLtMatrixLayout_t matLayout,
cudaDataType type,
int groupCount,
const void* rows_array,
const void* cols_array,
const void* ld_array);
Experimental: This function initializes a grouped matrix layout descriptor in a previously allocated one.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix layout descriptor initialized by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix layout descriptor this function initializes. See cudaDataType_t. |
|
|
Input |
Number of groups in the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of rows of the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of columns of the grouped matrix layout descriptor. |
|
|
Input |
Pointer to a device array of leading dimensions of the grouped matrix layout descriptor. |
Returns:
Return Value |
Description |
|---|---|
|
If the memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.39. cublasLtMatrixLayoutDestroy()
cublasStatus_t cublasLtMatrixLayoutDestroy(
cublasLtMatrixLayout_t matLayout);
This function destroys a previously created matrix layout descriptor object.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the structure holding the matrix layout descriptor that should be destroyed by this function. See cublasLtMatrixLayout_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the operation was successful. |
See cublasStatus_t for a complete list of valid return codes.
3.4.40. cublasLtMatrixLayoutGetAttribute()
cublasStatus_t cublasLtMatrixLayoutGetAttribute(
cublasLtMatrixLayout_t matLayout,
cublasLtMatrixLayoutAttribute_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried attribute belonging to the specified matrix layout descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix layout descriptor queried by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
The attribute being queried for. See cublasLtMatrixLayoutAttribute_t. |
|
|
Output |
The attribute value returned by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.41. cublasLtMatrixLayoutSetAttribute()
cublasStatus_t cublasLtMatrixLayoutSetAttribute(
cublasLtMatrixLayout_t matLayout,
cublasLtMatrixLayoutAttribute_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified attribute belonging to a previously created matrix layout descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix layout descriptor queried by this function. See cublasLtMatrixLayout_t. |
|
|
Input |
The attribute that will be set by this function. See cublasLtMatrixLayoutAttribute_t. |
|
|
Input |
The value to which the specified attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.42. cublasLtMatrixTransform()
cublasStatus_t cublasLtMatrixTransform(
cublasLtHandle_t lightHandle,
cublasLtMatrixTransformDesc_t transformDesc,
const void *alpha,
const void *A,
cublasLtMatrixLayout_t Adesc,
const void *beta,
const void *B,
cublasLtMatrixLayout_t Bdesc,
void *C,
cublasLtMatrixLayout_t Cdesc,
cudaStream_t stream);
This function computes the matrix transformation operation on the input matrices A and B, to produce the output matrix C, according to the below operation:
C = alpha*transformation(A) + beta*transformation(B),
where A, B are input matrices, and alpha and beta are input scalars. The transformation operation is defined by the transformDesc pointer. This function can be used to change the memory order of data or to scale and shift the values.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the allocated cuBLASLt handle for the cuBLASLt context. See cublasLtHandle_t. |
|
|
Input |
Pointer to the opaque descriptor holding the matrix transformation operation. See cublasLtMatrixTransformDesc_t. |
|
|
Device or host |
Input |
Pointers to the scalars used in the multiplication. |
|
Device |
Input |
Pointers to the GPU memory associated with the corresponding descriptors |
|
Device |
Output |
Pointer to the GPU memory associated with the |
|
Input |
Handles to the previous created descriptors of the type cublasLtMatrixLayout_t.
|
|
|
Host |
Input |
The CUDA stream where all the GPU work will be submitted. |
Returns:
Return Value |
Description |
|---|---|
|
If cuBLASLt handle has not been initialized. |
|
If the parameters are in conflict or in an impossible configuration. For example, when |
|
If the current implementation on the selected device does not support the configured operation. |
|
If the configured operation cannot be run using the selected device. |
|
If CUDA reported an execution error from the device. |
|
If the operation completed successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.43. cublasLtMatrixTransformDescCreate()
cublasStatus_t cublasLtMatrixTransformDescCreate(
cublasLtMatrixTransformDesc_t *transformDesc,
cudaDataType scaleType);
This function creates a matrix transform descriptor by allocating the memory needed to hold its opaque structure.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix transform descriptor created by this function. See cublasLtMatrixTransformDesc_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix transform descriptor this function creates. See cudaDataType_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.44. cublasLtMatrixTransformDescInit()
cublasStatus_t cublasLtMatrixTransformDescInit(
cublasLtMatrixTransformDesc_t transformDesc,
cudaDataType scaleType);
This function initializes a matrix transform descriptor in a previously allocated one.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Output |
Pointer to the structure holding the matrix transform descriptor initialized by this function. See cublasLtMatrixTransformDesc_t. |
|
|
Input |
Enumerant that specifies the data precision for the matrix transform descriptor this function initializes. See cudaDataType_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.45. cublasLtMatrixTransformDescDestroy()
cublasStatus_t cublasLtMatrixTransformDescDestroy(
cublasLtMatrixTransformDesc_t transformDesc);
This function destroys a previously created matrix transform descriptor object.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the structure holding the matrix transform descriptor that should be destroyed by this function. See cublasLtMatrixTransformDesc_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the operation was successful. |
See cublasStatus_t for a complete list of valid return codes.
3.4.46. cublasLtMatrixTransformDescGetAttribute()
cublasStatus_t cublasLtMatrixTransformDescGetAttribute(
cublasLtMatrixTransformDesc_t transformDesc,
cublasLtMatrixTransformDescAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried attribute belonging to a previously created matrix transform descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix transform descriptor queried by this function. See cublasLtMatrixTransformDesc_t. |
|
|
Input |
The attribute that will be retrieved by this function. See cublasLtMatrixTransformDescAttributes_t. |
|
|
Output |
Memory address containing the attribute value retrieved by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
|
|
If attribute’s value was successfully written to user memory. |
See cublasStatus_t for a complete list of valid return codes.
3.4.47. cublasLtMatrixTransformDescSetAttribute()
cublasStatus_t cublasLtMatrixTransformDescSetAttribute(
cublasLtMatrixTransformDesc_t transformDesc,
cublasLtMatrixTransformDescAttributes_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified attribute belonging to a previously created matrix transform descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the matrix transform descriptor queried by this function. See cublasLtMatrixTransformDesc_t. |
|
|
Input |
The attribute that will be set by this function. See cublasLtMatrixTransformDescAttributes_t. |
|
|
Input |
The value to which the specified attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If the attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.48. cublasLtEmulationDescInit()
cublasStatus_t cublasLtEmulationDescInit(cublasLtEmulationDesc_t emulationDesc);
This function initializes a previously allocated emulation descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the emulation descriptor queried by this function. See cublasLtEmulationDesc_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the size of the pre-allocated space is insufficient. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.49. cublasLtEmulationDescCreate()
cublasStatus_t cublasLtEmulationDescCreate(cublasLtEmulationDesc_t* emulationDesc);
This function creates a new emulation descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the emulation descriptor queried by this function. See cublasLtEmulationDesc_t. |
Returns:
Return Value |
Description |
|---|---|
|
If memory could not be allocated. |
|
If the descriptor was created successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.50. cublasLtEmulationDescDestroy()
cublasStatus_t cublasLtEmulationDescDestroy(cublasLtEmulationDesc_t emulationDesc);
This function destroys a previously created emulation descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the emulation descriptor queried by this function. See cublasLtEmulationDesc_t. |
Returns:
Return Value |
Description |
|---|---|
|
If the descriptor was destroyed successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.51. cublasLtEmulationDescSetAttribute()
cublasStatus_t cublasLtEmulationDescSetAttribute(
cublasLtEmulationDesc_t emulationDesc,
cublasLtEmulationDescAttributes_t attr,
const void *buf,
size_t sizeInBytes);
This function sets the value of the specified attribute belonging to a previously created emulation descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the emulation descriptor queried by this function. See cublasLtEmulationDesc_t. |
|
|
Input |
The attribute that will be set by this function. See cublasLtEmulationDescAttributes_t. |
|
|
Input |
The value to which the specified attribute should be set. |
|
|
Input |
Size of |
Returns:
Return Value |
Description |
|---|---|
|
If |
|
If the attribute was set successfully. |
See cublasStatus_t for a complete list of valid return codes.
3.4.52. cublasLtEmulationDescGetAttribute()
cublasStatus_t cublasLtEmulationDescGetAttribute(
cublasLtEmulationDesc_t emulationDesc,
cublasLtEmulationDescAttributes_t attr,
void *buf,
size_t sizeInBytes,
size_t *sizeWritten);
This function returns the value of the queried attribute belonging to a previously created emulation descriptor.
Parameters:
Parameter |
Memory |
Input / Output |
Description |
|---|---|---|---|
|
Input |
Pointer to the previously created structure holding the emulation descriptor queried by this function. See cublasLtEmulationDesc_t. |
|
|
Input |
The attribute that will be retrieved by this function. See cublasLtEmulationDescAttributes_t. |
|
|
Output |
Memory address containing the attribute value retrieved by this function. |
|
|
Input |
Size of |
|
|
Output |
Valid only when the return value is |
Returns:
Return Value |
Description |
|---|---|
|
If
|
|
If attribute’s value was successfully written to user memory. |
4. Using the cuBLASXt API
4.1. General description
The cuBLASXt API of cuBLAS exposes a multi-GPU capable host interface: when using this API the application only needs to allocate the required matrices on the host memory space. Additionally, the current implementation supports managed memory on Linux with GPU devices that have compute capability 6.x or greater but treats it as host memory. Managed memory is not supported on Windows. There are no restriction on the sizes of the matrices as long as they can fit into the host memory. The cuBLASXt API takes care of allocating the memory across the designated GPUs and dispatched the workload between them and finally retrieves the results back to the host. The cuBLASXt API supports only the compute-intensive BLAS3 routines (e.g matrix-matrix operations) where the PCI transfers back and forth from the GPU can be amortized. The cuBLASXt API has its own header file cublasXt.h.
Starting with release 8.0, cuBLASXt API allows any of the matrices to be located on a GPU device.
Note
When providing matrices allocated on the GPU using the Stream Ordered Memory Allocator, ensure visibility across all devices by using cudaMemPoolSetAccess.
Note
The cuBLASXt API is only supported on 64-bit platforms.
4.1.1. Tiling design approach
To be able to share the workload between multiple GPUs, the cuBLASXt API uses a tiling strategy : every matrix is divided in square tiles of user-controllable dimension BlockDim x BlockDim. The resulting matrix tiling defines the static scheduling policy : each resulting tile is affected to a GPU in a round robin fashion One CPU thread is created per GPU and is responsible to do the proper memory transfers and cuBLAS operations to compute all the tiles that it is responsible for. From a performance point of view, due to this static scheduling strategy, it is better that compute capabilities and PCI bandwidth are the same for every GPU. The figure below illustrates the tiles distribution between 3 GPUs. To compute the first tile G0 from C, the CPU thread 0 responsible of GPU0, have to load 3 tiles from the first row of A and tiles from the first column of B in a pipeline fashion in order to overlap memory transfer and computations and sum the results into the first tile G0 of C before to move on to the next tile G0.

Example of cublasXt<t>gemm() tiling for 3 Gpus
When the tile dimension is not an exact multiple of the dimensions of C, some tiles are partially filled on the right border or/and the bottom border. The current implementation does not pad the incomplete tiles but simply keep track of those incomplete tiles by doing the right reduced cuBLAS operations : this way, no extra computation is done. However it still can lead to some load unbalance when all GPUS do not have the same number of incomplete tiles to work on.
When one or more matrices are located on some GPU devices, the same tiling approach and workload sharing is applied. The memory transfers are in this case done between devices. However, when the computation of a tile and some data are located on the same GPU device, the memory transfer to/from the local data into tiles is bypassed and the GPU operates directly on the local data. This can lead to a significant performance increase, especially when only one GPU is used for the computation.
The matrices can be located on any GPU device, and do not have to be located on the same GPU device. Furthermore, the matrices can even be located on a GPU device that do not participate to the computation.
On the contrary of the cuBLAS API, even if all matrices are located on the same device, the cuBLASXt API is still a blocking API from the host point of view : the data results wherever located will be valid on the call return and no device synchronization is required.
4.1.2. Hybrid CPU-GPU computation
In the case of very large problems, the cuBLASXt API offers the possibility to offload some of the computation to the host CPU. This feature can be setup with the routines cublasXtSetCpuRoutine() and cublasXtSetCpuRatio() The workload affected to the CPU is put aside : it is simply a percentage of the resulting matrix taken from the bottom and the right side whichever dimension is bigger. The GPU tiling is done after that on the reduced resulting matrix.
If any of the matrices is located on a GPU device, the feature is ignored and all computation will be done only on the GPUs
This feature should be used with caution because it could interfere with the CPU threads responsible of feeding the GPUs.
Currently, only the routine cublasXt<t>gemm() supports this feature.
4.1.3. Results reproducibility
Currently all cuBLASXt API routines from a given toolkit version, generate the same bit-wise results when the following conditions are respected :
all GPUs participating to the computation have the same compute capabilities and the same number of SMs.
the tiles size is kept the same between run.
either the CPU hybrid computation is not used or the CPU Blas provided is also guaranteed to produce reproducible results.
4.2. cuBLASXt API Datatypes Reference
4.2.1. cublasXtHandle_t
The cublasXtHandle_t type is a pointer type to an opaque structure holding the cuBLASXt API context. The cuBLASXt API context must be initialized using cublasXtCreate() and the returned handle must be passed to all subsequent cuBLASXt API function calls. The context should be destroyed at the end using cublasXtDestroy().
4.2.2. cublasXtOpType_t
The cublasOpType_t enumerates the four possible types supported by BLAS routines. This enum is used as parameters of the routines cublasXtSetCpuRoutine and cublasXtSetCpuRatio to setup the hybrid configuration.
Value |
Meaning |
|---|---|
|
float or single precision type |
|
double precision type |
|
single precision complex |
|
double precision complex |
4.2.3. cublasXtBlasOp_t
The cublasXtBlasOp_t type enumerates the BLAS3 or BLAS-like routine supported by cuBLASXt API. This enum is used as parameters of the routines cublasXtSetCpuRoutine and cublasXtSetCpuRatio to setup the hybrid configuration.
Value |
Meaning |
|---|---|
|
GEMM routine |
|
SYRK routine |
|
HERK routine |
|
SYMM routine |
|
HEMM routine |
|
TRSM routine |
|
SYR2K routine |
|
HER2K routine |
|
SPMM routine |
|
SYRKX routine |
|
HERKX routine |
4.2.4. cublasXtPinningMemMode_t
The type is used to enable or disable the Pinning Memory mode through the routine cubasMgSetPinningMemMode
Value |
Meaning |
|---|---|
|
the Pinning Memory mode is disabled |
|
the Pinning Memory mode is enabled |
4.3. cuBLASXt API Helper Function Reference
4.3.1. cublasXtCreate()
cublasStatus_t
cublasXtCreate(cublasXtHandle_t *handle)
This function initializes the cuBLASXt API and creates a handle to an opaque structure holding the cuBLASXt API context. It allocates hardware resources on the host and device and must be called prior to making any other cuBLASXt API calls.
Return Value |
Meaning |
|---|---|
|
the initialization succeeded |
|
the resources could not be allocated |
|
cuBLASXt API is only supported on 64-bit platform |
4.3.2. cublasXtDestroy()
cublasStatus_t
cublasXtDestroy(cublasXtHandle_t handle)
This function releases hardware resources used by the cuBLASXt API context. The release of GPU resources may be deferred until the application exits. This function is usually the last call with a particular handle to the cuBLASXt API.
Return Value |
Meaning |
|---|---|
|
the shut down succeeded |
|
the library was not initialized |
4.3.3. cublasXtDeviceSelect()
cublasXtDeviceSelect(cublasXtHandle_t handle, int nbDevices, int deviceId[])
This function allows the user to provide the number of GPU devices and their respective Ids that will participate to the subsequent cuBLASXt API Math function calls. This function will create a cuBLAS context for every GPU provided in that list. Currently the device configuration is static and cannot be changed between Math function calls. In that regard, this function should be called only once after cublasXtCreate. To be able to run multiple configurations, multiple cuBLASXt API contexts should be created.
Return Value |
Meaning |
|---|---|
|
User call was successful |
|
Access to at least one of the device could not be done or a cuBLAS context could not be created on at least one of the device |
|
Some resources could not be allocated. |
4.3.4. cublasXtSetBlockDim()
cublasXtSetBlockDim(cublasXtHandle_t handle, int blockDim)
This function allows the user to set the block dimension used for the tiling of the matrices for the subsequent Math function calls. Matrices are split in square tiles of blockDim x blockDim dimension. This function can be called anytime and will take effect for the following Math function calls. The block dimension should be chosen in a way to optimize the math operation and to make sure that the PCI transfers are well overlapped with the computation.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
|
blockDim <= 0 |
4.3.5. cublasXtGetBlockDim()
cublasXtGetBlockDim(cublasXtHandle_t handle, int *blockDim)
This function allows the user to query the block dimension used for the tiling of the matrices.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
4.3.6. cublasXtSetCpuRoutine()
cublasXtSetCpuRoutine(cublasXtHandle_t handle, cublasXtBlasOp_t blasOp, cublasXtOpType_t type, void *blasFunctor)
This function allows the user to provide a CPU implementation of the corresponding BLAS routine. This function can be used with the function cublasXtSetCpuRatio() to define an hybrid computation between the CPU and the GPUs. Currently the hybrid feature is only supported for the xGEMM routines.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
|
blasOp or type define an invalid combination |
|
CPU-GPU Hybridization for that routine is not supported |
4.3.7. cublasXtSetCpuRatio()
cublasXtSetCpuRatio(cublasXtHandle_t handle, cublasXtBlasOp_t blasOp, cublasXtOpType_t type, float ratio )
This function allows the user to define the percentage of workload that should be done on a CPU in the context of an hybrid computation. This function can be used with the function cublasXtSetCpuRoutine() to define an hybrid computation between the CPU and the GPUs. Currently the hybrid feature is only supported for the xGEMM routines.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
|
blasOp or type define an invalid combination |
|
CPU-GPU Hybridization for that routine is not supported |
4.3.8. cublasXtSetPinningMemMode()
cublasXtSetPinningMemMode(cublasXtHandle_t handle, cublasXtPinningMemMode_t mode)
This function allows the user to enable or disable the Pinning Memory mode. When enabled, the matrices passed in subsequent cuBLASXt API calls will be pinned/unpinned using the CUDART routine cudaHostRegister() and cudaHostUnregister() respectively if the matrices are not already pinned. If a matrix happened to be pinned partially, it will also not be pinned. Pinning the memory improve PCI transfer performance and allows to overlap PCI memory transfer with computation. However pinning/unpinning the memory take some time which might not be amortized. It is advised that the user pins the memory on its own using cudaMallocHost() or cudaHostRegister() and unpin it when the computation sequence is completed. By default, the Pinning Memory mode is disabled.
Note
The Pinning Memory mode should not be enabled when matrices used for different calls to cuBLASXt API overlap. cuBLASXt determines that a matrix is pinned or not if the first address of that matrix is pinned using cudaHostGetFlags(), thus cannot know if the matrix is already partially pinned or not. This is especially true in multi-threaded application where memory could be partially or totally pinned or unpinned while another thread is accessing that memory.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
|
the mode value is different from |
4.3.9. cublasXtGetPinningMemMode()
cublasXtGetPinningMemMode(cublasXtHandle_t handle, cublasXtPinningMemMode_t *mode)
This function allows the user to query the Pinning Memory mode. By default, the Pinning Memory mode is disabled.
Return Value |
Meaning |
|---|---|
|
the call has been successful |
4.4. cuBLASXt API Math Functions Reference
In this chapter we describe the actual Linear Algebra routines that cuBLASXt API supports. We will use abbreviations <type> for type and <t> for the corresponding short type to make a more concise and clear presentation of the implemented functions. Unless otherwise specified <type> and <t> have the following meanings:
<type> |
<t> |
Meaning |
|---|---|---|
|
‘s’ or ‘S’ |
real single-precision |
|
‘d’ or ‘D’ |
real double-precision |
|
‘c’ or ‘C’ |
complex single-precision |
|
‘z’ or ‘Z’ |
complex double-precision |
The abbreviation \(\mathbf{Re}(\cdot)\) and \(\mathbf{Im}(\cdot)\) will stand for the real and imaginary part of a number, respectively. Since imaginary part of a real number does not exist, we will consider it to be zero and can usually simply discard it from the equation where it is being used. Also, the \(\bar{\alpha}\) will denote the complex conjugate of \(\alpha\) .
In general throughout the documentation, the lower case Greek symbols \(\alpha\) and \(\beta\) will denote scalars, lower case English letters in bold type \(\mathbf{x}\) and \(\mathbf{y}\) will denote vectors and capital English letters \(A\) , \(B\) and \(C\) will denote matrices.
4.4.1. cublasXt<t>gemm()
cublasStatus_t cublasXtSgemm(cublasXtHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
size_t m, size_t n, size_t k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasXtDgemm(cublasXtHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const double *alpha,
const double *A, int lda,
const double *B, int ldb,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasXtCgemm(cublasXtHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *B, int ldb,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasXtZgemm(cublasXtHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *B, int ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function performs the matrix-matrix multiplication
\(C = \alpha\text{op}(A)\text{op}(B) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, and \(A\) , \(B\) and \(C\) are matrices stored in column-major format with dimensions \(\text{op}(A)\) \(m \times k\) , \(\text{op}(B)\) \(k \times n\) and \(C\) \(m \times n\) , respectively. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
and \(\text{op}(B)\) is defined similarly for matrix \(B\) .
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
operation op( |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
input |
number of columns of op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store the matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication. If |
|
host or device |
in/out |
<type> array of dimensions |
|
input |
leading dimension of a two-dimensional array used to store the matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.2. cublasXt<t>hemm()
cublasStatus_t cublasXtChemm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const cuComplex *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZhemm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, size_t ldc)
This function performs the Hermitian matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha AB + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha BA + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a Hermitian matrix stored in lower or upper mode, \(B\) and \(C\) are \(m \times n\) matrices, and \(\alpha\) and \(\beta\) are scalars.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
indicates if matrix |
|
|
input |
number of rows of matrix |
|
|
input |
number of columns of matrix |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.3. cublasXt<t>symm()
cublasStatus_t cublasXtSsymm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const float *alpha,
const float *A, size_t lda,
const float *B, size_t ldb,
const float *beta,
float *C, size_t ldc)
cublasStatus_t cublasXtDsymm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const double *alpha,
const double *A, size_t lda,
const double *B, size_t ldb,
const double *beta,
double *C, size_t ldc)
cublasStatus_t cublasXtCsymm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const cuComplex *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZsymm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
size_t m, size_t n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, size_t ldc)
This function performs the symmetric matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha AB + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha BA + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a symmetric matrix stored in lower or upper mode, \(A\) and \(A\) are \(m \times n\) matrices, and \(\alpha\) and \(\beta\) are scalars.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
indicates if matrix |
|
|
input |
number of rows of matrix |
|
|
input |
number of columns of matrix |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.4. cublasXt<t>syrk()
cublasStatus_t cublasXtSsyrk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const float *A, int lda,
const float *beta,
float *C, int ldc)
cublasStatus_t cublasXtDsyrk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const double *A, int lda,
const double *beta,
double *C, int ldc)
cublasStatus_t cublasXtCsyrk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuComplex *alpha,
const cuComplex *A, int lda,
const cuComplex *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasXtZsyrk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, int lda,
const cuDoubleComplex *beta,
cuDoubleComplex *C, int ldc)
This function performs the symmetric rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix A. |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.5. cublasXt<t>syr2k()
cublasStatus_t cublasXtSsyr2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const float *alpha,
const float *A, size_t lda,
const float *B, size_t ldb,
const float *beta,
float *C, size_t ldc)
cublasStatus_t cublasXtDsyr2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const double *alpha,
const double *A, size_t lda,
const double *B, size_t ldb,
const double *beta,
double *C, size_t ldc)
cublasStatus_t cublasXtCsyr2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const cuComplex *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZsyr2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, size_t ldc)
This function performs the symmetric rank- \(2k\) update
\(C = \alpha(\text{op}(A)\text{op}(B)^{T} + \text{op}(B)\text{op}(A)^{T}) + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\text{ and }B^{T}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.6. cublasXt<t>syrkx()
cublasStatus_t cublasXtSsyrkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const float *alpha,
const float *A, size_t lda,
const float *B, size_t ldb,
const float *beta,
float *C, size_t ldc)
cublasStatus_t cublasXtDsyrkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const double *alpha,
const double *A, size_t lda,
const double *B, size_t ldb,
const double *beta,
double *C, size_t ldc)
cublasStatus_t cublasXtCsyrkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const cuComplex *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZsyrkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C, size_t ldc)
This function performs a variation of the symmetric rank- \(k\) update
\(C = \alpha(\text{op}(A)\text{op}(B)^{T} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a symmetric matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{T}\text{ and }B^{T}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_T}$}} \\ \end{matrix} \right.\)
This routine can be used when B is in such way that the result is guaranteed to be symmetric. A usual example is when the matrix B is a scaled form of the matrix A : this is equivalent to B being the product of the matrix A and a diagonal matrix.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.7. cublasXt<t>herk()
cublasStatus_t cublasXtCherk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const float *alpha,
const cuComplex *A, int lda,
const float *beta,
cuComplex *C, int ldc)
cublasStatus_t cublasXtZherk(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
int n, int k,
const double *alpha,
const cuDoubleComplex *A, int lda,
const double *beta,
cuDoubleComplex *C, int ldc)
This function performs the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) is a matrix with dimensions \(\text{op}(A)\) \(n \times k\) . Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.8. cublasXt<t>her2k()
cublasStatus_t cublasXtCher2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const float *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZher2k(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const double *beta,
cuDoubleComplex *C, size_t ldc)
This function performs the Hermitian rank- \(2k\) update
\(C = \alpha\text{op}(A)\text{op}(B)^{H} + \overset{ˉ}{\alpha}\text{op}(B)\text{op}(A)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{H}\text{ and }B^{H}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.9. cublasXt<t>herkx()
cublasStatus_t cublasXtCherkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
const float *beta,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZherkx(cublasXtHandle_t handle,
cublasFillMode_t uplo, cublasOperation_t trans,
size_t n, size_t k,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
const double *beta,
cuDoubleComplex *C, size_t ldc)
This function performs a variation of the Hermitian rank- \(k\) update
\(C = \alpha\text{op}(A)\text{op}(B)^{H} + \beta C\)
where \(\alpha\) and \(\beta\) are scalars, \(C\) is a Hermitian matrix stored in lower or upper mode, and \(A\) and \(B\) are matrices with dimensions \(\text{op}(A)\) \(n \times k\) and \(\text{op}(B)\) \(n \times k\) , respectively. Also, for matrix \(A\) and \(B\)
\(\text{op(}A\text{) and op(}B\text{)} = \left\{ \begin{matrix} {A\text{ and }B} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_N}$}} \\ {A^{H}\text{ and }B^{H}} & {\text{if }\textsf{trans == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
This routine can be used when the matrix B is in such way that the result is guaranteed to be hermitian. A usual example is when the matrix B is a scaled form of the matrix A : this is equivalent to B being the product of the matrix A and a diagonal matrix.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
number of rows of matrix op( |
|
|
input |
number of columns of matrix op( |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
real scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.10. cublasXt<t>trsm()
cublasStatus_t cublasXtStrsm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasXtDiagType_t diag,
size_t m, size_t n,
const float *alpha,
const float *A, size_t lda,
float *B, size_t ldb)
cublasStatus_t cublasXtDtrsm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasXtDiagType_t diag,
size_t m, size_t n,
const double *alpha,
const double *A, size_t lda,
double *B, size_t ldb)
cublasStatus_t cublasXtCtrsm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasXtDiagType_t diag,
size_t m, size_t n,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
cuComplex *B, size_t ldb)
cublasStatus_t cublasXtZtrsm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasXtDiagType_t diag,
size_t m, size_t n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
cuDoubleComplex *B, size_t ldb)
This function solves the triangular linear system with multiple right-hand-sides
\(\left\{ \begin{matrix} {\text{op}(A)X = \alpha B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {X\text{op}(A) = \alpha B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, \(X\) and \(B\) are \(m \times n\) matrices, and \(\alpha\) is a scalar. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
The solution \(X\) overwrites the right-hand-sides \(B\) on exit.
No test for singularity or near-singularity is included in this function.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
indicates if the elements on the main diagonal of matrix |
|
|
input |
number of rows of matrix |
|
|
input |
number of columns of matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
in/out |
<type> array. It has dimensions |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.11. cublasXt<t>trmm()
cublasStatus_t cublasXtStrmm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
size_t m, size_t n,
const float *alpha,
const float *A, size_t lda,
const float *B, size_t ldb,
float *C, size_t ldc)
cublasStatus_t cublasXtDtrmm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
size_t m, size_t n,
const double *alpha,
const double *A, size_t lda,
const double *B, size_t ldb,
double *C, size_t ldc)
cublasStatus_t cublasXtCtrmm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
size_t m, size_t n,
const cuComplex *alpha,
const cuComplex *A, size_t lda,
const cuComplex *B, size_t ldb,
cuComplex *C, size_t ldc)
cublasStatus_t cublasXtZtrmm(cublasXtHandle_t handle,
cublasSideMode_t side, cublasFillMode_t uplo,
cublasOperation_t trans, cublasDiagType_t diag,
size_t m, size_t n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *A, size_t lda,
const cuDoubleComplex *B, size_t ldb,
cuDoubleComplex *C, size_t ldc)
This function performs the triangular matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha\text{op}(A)B} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha B\text{op}(A)} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a triangular matrix stored in lower or upper mode with or without the main diagonal, \(B\) and \(C\) are \(m \times n\) matrix, and \(\alpha\) is a scalar. Also, for matrix \(A\)
\(\text{op}(A) = \left\{ \begin{matrix} A & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_N}$}} \\ A^{T} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_T}$}} \\ A^{H} & {\text{if }\textsf{transa == $\mathrm{CUBLAS\_OP\_C}$}} \\ \end{matrix} \right.\)
Notice that in order to achieve better parallelism, similarly to the cublas API, cuBLASXt API differs from the BLAS API for this routine. The BLAS API assumes an in-place implementation (with results written back to B), while the cuBLASXt API assumes an out-of-place implementation (with results written into C). The application can still obtain the in-place functionality of BLAS in the cuBLASXt API by passing the address of the matrix B in place of the matrix C. No other overlapping in the input parameters is supported.
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
indicates if matrix |
|
|
input |
operation op( |
|
|
input |
indicates if the elements on the main diagonal of matrix |
|
|
input |
number of rows of matrix |
|
|
input |
number of columns of matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
4.4.12. cublasXt<t>spmm()
cublasStatus_t cublasXtSspmm( cublasXtHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
size_t m,
size_t n,
const float *alpha,
const float *AP,
const float *B,
size_t ldb,
const float *beta,
float *C,
size_t ldc );
cublasStatus_t cublasXtDspmm( cublasXtHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
size_t m,
size_t n,
const double *alpha,
const double *AP,
const double *B,
size_t ldb,
const double *beta,
double *C,
size_t ldc );
cublasStatus_t cublasXtCspmm( cublasXtHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
size_t m,
size_t n,
const cuComplex *alpha,
const cuComplex *AP,
const cuComplex *B,
size_t ldb,
const cuComplex *beta,
cuComplex *C,
size_t ldc );
cublasStatus_t cublasXtZspmm( cublasXtHandle_t handle,
cublasSideMode_t side,
cublasFillMode_t uplo,
size_t m,
size_t n,
const cuDoubleComplex *alpha,
const cuDoubleComplex *AP,
const cuDoubleComplex *B,
size_t ldb,
const cuDoubleComplex *beta,
cuDoubleComplex *C,
size_t ldc );
This function performs the symmetric packed matrix-matrix multiplication
\(C = \left\{ \begin{matrix} {\alpha AB + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_LEFT}$}} \\ {\alpha BA + \beta C} & {\text{if }\textsf{side == $\mathrm{CUBLAS\_SIDE\_RIGHT}$}} \\ \end{matrix} \right.\)
where \(A\) is a \(n \times n\) symmetric matrix stored in packed format, \(B\) and \(C\) are \(m \times n\) matrices, and \(\alpha\) and \(\beta\) are scalars.
If uplo == CUBLAS_FILL_MODE_LOWER then the elements in the lower triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+((2*n-j+1)*j)/2] for \(j = 1,\ldots,n\) and \(i \geq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
If uplo == CUBLAS_FILL_MODE_UPPER then the elements in the upper triangular part of the symmetric matrix \(A\) are packed together column by column without gaps, so that the element \(A(i,j)\) is stored in the memory location AP[i+(j*(j+1))/2] for \(j = 1,\ldots,n\) and \(i \leq j\) . Consequently, the packed format requires only \(\frac{n(n + 1)}{2}\) elements for storage.
Note
The packed matrix AP must be located on the host or managed memory whereas the other matrices can be located on the host or any GPU device
Param. |
Memory |
In/out |
Meaning |
|---|---|---|---|
|
input |
handle to the cuBLASXt API context. |
|
|
input |
indicates if matrix |
|
|
input |
indicates if matrix |
|
|
input |
number of rows of matrix |
|
|
input |
number of columns of matrix |
|
|
host |
input |
<type> scalar used for multiplication. |
|
host |
input |
<type> array with \(A\) stored in packed format. |
|
host or device |
input |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
|
|
host |
input |
<type> scalar used for multiplication, if |
|
host or device |
in/out |
<type> array of dimension |
|
input |
leading dimension of two-dimensional array used to store matrix |
The possible error values returned by this function and their meanings are listed below.
Error Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the parameters |
|
the matrix AP is located on a GPU device |
|
the function failed to launch on the GPU |
For references please refer to NETLIB documentation:
5. Using the cuBLASDx API
The cuBLASDx library (preview) is a device side API extension for performing BLAS calculations inside CUDA kernels. By fusing numerical operations you can decrease latency and further improve performance of your applications.
6. Using the cuBLAS Legacy API
This section does not provide a full reference of each Legacy API datatype and entry point. Instead, it describes how to use the API, especially where this is different from the regular cuBLAS API.
Note that in this section, all references to the “cuBLAS Library” refer to the Legacy cuBLAS API only.
Warning
The legacy cuBLAS API is deprecated and will be removed in future release.
6.1. Error Status
The cublasStatus type is used for function status returns. The cuBLAS Library helper functions return status directly, while the status of core functions can be retrieved using cublasGetError(). Notice that reading the error status via cublasGetError(), resets the internal error state to CUBLAS_STATUS_SUCCESS. Currently, the following values are defined:
Value |
Meaning |
|---|---|
|
the operation completed successfully |
|
the library was not initialized |
|
the resource allocation failed |
|
an invalid numerical value was used as an argument |
|
an absent device architectural feature is required |
|
an access to GPU memory space failed |
|
the GPU program failed to execute |
|
an internal operation failed |
|
the feature required is not supported |
This legacy type corresponds to type cublasStatus_t in the cuBLAS library API.
6.2. Initialization and Shutdown
The functions cublasInit() and cublasShutdown() are used to initialize and shutdown the cuBLAS library. It is recommended for cublasInit() to be called before any other function is invoked. It allocates hardware resources on the GPU device that is currently bound to the host thread from which it was invoked.
The legacy initialization and shutdown functions are similar to the cuBLAS library API routines cublasCreate() and cublasDestroy().
6.3. Thread Safety
The legacy API is not thread safe when used with multiple host threads and devices. It is recommended to be used only when utmost compatibility with Fortran is required and when a single host thread is used to setup the library and make all the functions calls.
6.4. Memory Management
The memory used by the legacy cuBLAS library API is allocated and released using functions cublasAlloc() and cublasFree(), respectively. These functions create and destroy an object in the GPU memory space capable of holding an array of n elements, where each element requires elemSize bytes of storage. Please see the legacy cuBLAS API header file “cublas.h” for the prototypes of these functions.
The function cublasAlloc() is a wrapper around the function cudaMalloc(), therefore device pointers returned by cublasAlloc() can be passed to any CUDA™ device kernel functions. However, these device pointers can not be dereferenced in the host code. The function cublasFree() is a wrapper around the function cudaFree().
6.5. Scalar Parameters
In the legacy cuBLAS API, scalar parameters are passed by value from the host. Also, the few functions that do return a scalar result, such as dot() and nrm2(), return the resulting value on the host, and hence these routines will wait for kernel execution on the device to complete before returning, which makes parallelism with streams impractical. However, the majority of functions do not return any value, in order to be more compatible with Fortran and the existing BLAS libraries.
6.6. Helper Functions
In this section we list the helper functions provided by the legacy cuBLAS API and their functionality. For the exact prototypes of these functions please refer to the legacy cuBLAS API header file “cublas.h”.
Helper function |
Meaning |
|---|---|
|
initialize the library |
|
shuts down the library |
|
retrieves the error status of the library |
|
sets the stream to be used by the library |
|
allocates the device memory for the library |
|
releases the device memory allocated for the library |
|
copies a vector |
|
copies a vector |
|
copies a \(m \times n\) tile from a matrix on the host to the GPU |
|
copies a \(m \times n\) tile from a matrix on the GPU to the host |
|
similar to |
|
similar to |
|
similar to |
|
similar to |
6.7. Level-1,2,3 Functions
The Level-1,2,3 cuBLAS functions (also called core functions) have the same name and behavior as the ones listed in the chapters 3, 4 and 5 in this document. Please refer to the legacy cuBLAS API header file “cublas.h” for their exact prototype. Also, the next section talks a bit more about the differences between the legacy and the cuBLAS API prototypes, more specifically how to convert the function calls from one API to another.
6.8. Converting Legacy to the cuBLAS API
There are a few general rules that can be used to convert from legacy to the cuBLAS API:
Exchange the header file “cublas.h” for “cublas_v2.h”.
Exchange the type
cublasStatusfor cublasStatus_t.Exchange the function
cublasSetKernelStream()for cublasSetStream().Exchange the function
cublasAlloc()andcublasFree()forcudaMalloc()andcudaFree(), respectively. Notice thatcudaMalloc()expects the size of the allocated memory to be provided in bytes (usually simply providen x elemSizeto allocatenelements, each of sizeelemSizebytes).Declare the
cublasHandle_tcuBLAS library handle.Initialize the handle using cublasCreate(). Also, release the handle once finished using cublasDestroy().
Add the handle as the first parameter to all the cuBLAS library function calls.
Change the scalar parameters to be passed by reference, instead of by value (usually simply adding “&” symbol in C/C++ is enough, because the parameters are passed by reference on the host by default). However, note that if the routine is running asynchronously, then the variable holding the scalar parameter cannot be changed until the kernels that the routine dispatches are completed. See the CUDA C++ Programming Guide for a detailed discussion of how to use streams.
Change the parameter characters
Norn(non-transpose operation),Tort(transpose operation) andCorc(conjugate transpose operation) toCUBLAS_OP_N,CUBLAS_OP_TandCUBLAS_OP_C, respectively.Change the parameter characters
Lorl(lower part filled) andUoru(upper part filled) toCUBLAS_FILL_MODE_LOWERandCUBLAS_FILL_MODE_UPPER, respectively.Change the parameter characters
Norn(non-unit diagonal) andUoru(unit diagonal) toCUBLAS_DIAG_NON_UNITandCUBLAS_DIAG_UNIT, respectively.Change the parameter characters
Lorl(left side) andRorr(right side) toCUBLAS_SIDE_LEFTandCUBLAS_SIDE_RIGHT, respectively.If the legacy API function returns a scalar value, add an extra scalar parameter of the same type passed by reference, as the last parameter to the same function.
Instead of using
cublasGetError(), use the return value of the function itself to check for errors.Finally, please use the function prototypes in the header files
cublas.handcublas_v2.hto check the code for correctness.
6.9. Examples
For sample code references that use the legacy cuBLAS API please see the two examples below. They show an application written in C using the legacy cuBLAS library API with two indexing styles (Example A.1. “Application Using C and cuBLAS: 1-based indexing” and Example A.2. “Application Using C and cuBLAS: 0-based Indexing”). This application is analogous to the one using the cuBLAS library API that is shown in the Introduction chapter.
Example A.1. Application Using C and cuBLAS: 1-based indexing
//-----------------------------------------------------------
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "cublas.h"
#define M 6
#define N 5
#define IDX2F(i,j,ld) ((((j)-1)*(ld))+((i)-1))
static __inline__ void modify (float *m, int ldm, int n, int p, int q, float alpha, float beta){
cublasSscal (n-q+1, alpha, &m[IDX2F(p,q,ldm)], ldm);
cublasSscal (ldm-p+1, beta, &m[IDX2F(p,q,ldm)], 1);
}
int main (void){
int i, j;
cublasStatus stat;
float* devPtrA;
float* a = 0;
a = (float *)malloc (M * N * sizeof (*a));
if (!a) {
printf ("host memory allocation failed");
return EXIT_FAILURE;
}
for (j = 1; j <= N; j++) {
for (i = 1; i <= M; i++) {
a[IDX2F(i,j,M)] = (float)((i-1) * M + j);
}
}
cublasInit();
stat = cublasAlloc (M*N, sizeof(*a), (void**)&devPtrA);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("device memory allocation failed");
cublasShutdown();
return EXIT_FAILURE;
}
stat = cublasSetMatrix (M, N, sizeof(*a), a, M, devPtrA, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data download failed");
cublasFree (devPtrA);
cublasShutdown();
return EXIT_FAILURE;
}
modify (devPtrA, M, N, 2, 3, 16.0f, 12.0f);
stat = cublasGetMatrix (M, N, sizeof(*a), devPtrA, M, a, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data upload failed");
cublasFree (devPtrA);
cublasShutdown();
return EXIT_FAILURE;
}
cublasFree (devPtrA);
cublasShutdown();
for (j = 1; j <= N; j++) {
for (i = 1; i <= M; i++) {
printf ("%7.0f", a[IDX2F(i,j,M)]);
}
printf ("\n");
}
free(a);
return EXIT_SUCCESS;
}
Example A.2. Application Using C and cuBLAS: 0-based indexing
//-----------------------------------------------------------
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "cublas.h"
#define M 6
#define N 5
#define IDX2C(i,j,ld) (((j)*(ld))+(i))
static __inline__ void modify (float *m, int ldm, int n, int p, int q, float alpha, float beta){
cublasSscal (n-q, alpha, &m[IDX2C(p,q,ldm)], ldm);
cublasSscal (ldm-p, beta, &m[IDX2C(p,q,ldm)], 1);
}
int main (void){
int i, j;
cublasStatus stat;
float* devPtrA;
float* a = 0;
a = (float *)malloc (M * N * sizeof (*a));
if (!a) {
printf ("host memory allocation failed");
return EXIT_FAILURE;
}
for (j = 0; j < N; j++) {
for (i = 0; i < M; i++) {
a[IDX2C(i,j,M)] = (float)(i * M + j + 1);
}
}
cublasInit();
stat = cublasAlloc (M*N, sizeof(*a), (void**)&devPtrA);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("device memory allocation failed");
cublasShutdown();
return EXIT_FAILURE;
}
stat = cublasSetMatrix (M, N, sizeof(*a), a, M, devPtrA, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data download failed");
cublasFree (devPtrA);
cublasShutdown();
return EXIT_FAILURE;
}
modify (devPtrA, M, N, 1, 2, 16.0f, 12.0f);
stat = cublasGetMatrix (M, N, sizeof(*a), devPtrA, M, a, M);
if (stat != CUBLAS_STATUS_SUCCESS) {
printf ("data upload failed");
cublasFree (devPtrA);
cublasShutdown();
return EXIT_FAILURE;
}
cublasFree (devPtrA);
cublasShutdown();
for (j = 0; j < N; j++) {
for (i = 0; i < M; i++) {
printf ("%7.0f", a[IDX2C(i,j,M)]);
}
printf ("\n");
}
free(a);
return EXIT_SUCCESS;
}
7. cuBLAS Fortran Bindings
The cuBLAS library is implemented using the C-based CUDA toolchain. Thus, it provides a C-style API. This makes interfacing to applications written in C and C++ trivial, but the library can also be used by applications written in Fortran. In particular, the cuBLAS library uses 1-based indexing and Fortran-style column-major storage for multidimensional data to simplify interfacing to Fortran applications. Unfortunately, Fortran-to-C calling conventions are not standardized and differ by platform and toolchain. In particular, differences may exist in the following areas:
symbol names (capitalization, name decoration)
argument passing (by value or reference)
passing of string arguments (length information)
passing of pointer arguments (size of the pointer)
returning floating-point or compound data types (for example single-precision or complex data types)
To provide maximum flexibility in addressing those differences, the cuBLAS Fortran interface is provided in the form of wrapper functions and is part of the Toolkit delivery. The C source code of those wrapper functions is located in the src directory and provided in two different forms:
the thunking wrapper interface located in the file
fortran_thunking.cthe direct wrapper interface located in the file
fortran.c
The code of one of those two files needs to be compiled into an application for it to call the cuBLAS API functions. Providing source code allows users to make any changes necessary for a particular platform and toolchain.
The code in those two C files has been used to demonstrate interoperability with the compilers g77 3.2.3 and g95 0.91 on 32-bit Linux, g77 3.4.5 and g95 0.91 on 64-bit Linux, Intel Fortran 9.0 and Intel Fortran 10.0 on 32-bit and 64-bit Microsoft Windows XP, and g77 3.4.0 and g95 0.92 on Mac OS X.
Note that for g77, use of the compiler flag -fno-second-underscore is required to use these wrappers as provided. Also, the use of the default calling conventions with regard to argument and return value passing is expected. Using the flag -fno-f2c changes the default calling convention with respect to these two items.
The thunking wrappers allow interfacing to existing Fortran applications without any changes to the application. During each call, the wrappers allocate GPU memory, copy source data from CPU memory space to GPU memory space, call cuBLAS, and finally copy back the results to CPU memory space and deallocate the GPU memory. As this process causes very significant call overhead, these wrappers are intended for light testing, not for production code. To use the thunking wrappers, the application needs to be compiled with the file fortran_thunking.c.
The direct wrappers, intended for production code, substitute device pointers for vector and matrix arguments in all BLAS functions. To use these interfaces, existing applications need to be modified slightly to allocate and deallocate data structures in GPU memory space (using cuBLAS_ALLOC and cuBLAS_FREE) and to copy data between GPU and CPU memory spaces (using cuBLAS_SET_VECTOR, cuBLAS_GET_VECTOR, cuBLAS_SET_MATRIX, and cuBLAS_GET_MATRIX). The sample wrappers provided in fortran.c map device pointers to the OS-dependent type size_t, which is 32-bit wide on 32-bit platforms and 64-bit wide on a 64-bit platforms.
One approach to deal with index arithmetic on device pointers in Fortran code is to use C-style macros, and use the C preprocessor to expand these, as shown in the example below. On Linux and Mac OS X, one way of pre-processing is to use the option -E -x f77-cpp-input when using g77 compiler, or simply the option -cpp when using g95 or gfortran. On Windows platforms with Microsoft Visual C/C++, using ’cl -EP’ achieves similar results.
! Example B.1. Fortran 77 Application Executing on the Host
! ----------------------------------------------------------
subroutine modify ( m, ldm, n, p, q, alpha, beta )
implicit none
integer ldm, n, p, q
real*4 m (ldm, *) , alpha , beta
external cublas_sscal
call cublas_sscal (n-p+1, alpha , m(p,q), ldm)
call cublas_sscal (ldm-p+1, beta, m(p,q), 1)
return
end
program matrixmod
implicit none
integer M,N
parameter (M=6, N=5)
real*4 a(M,N)
integer i, j
external cublas_init
external cublas_shutdown
do j = 1, N
do i = 1, M
a(i, j) = (i-1)*M + j
enddo
enddo
call cublas_init
call modify ( a, M, N, 2, 3, 16.0, 12.0 )
call cublas_shutdown
do j = 1 , N
do i = 1 , M
write(*,"(F7.0$)") a(i,j)
enddo
write (*,*) ""
enddo
stop
end
When traditional fixed-form Fortran 77 code is ported to use the cuBLAS library, line length often increases when the BLAS calls are exchanged for cuBLAS calls. Longer function names and possible macro expansion are contributing factors. Inadvertently exceeding the maximum line length can lead to run-time errors that are difficult to find, so care should be taken not to exceed the 72-column limit if fixed form is retained.
The examples in this chapter show a small application implemented in Fortran 77 on the host and the same application with the non-thunking wrappers after it has been ported to use the cuBLAS library.
The second example should be compiled with ARCH_64 defined as 1 on 64-bit OS system and as 0 on 32-bit OS system. For example for g95 or gfortran, this can be done directly on the command line by using the option -cpp -DARCH_64=1.
! Example B.2. Same Application Using Non-thunking cuBLAS Calls
!-------------------------------------------------------------
#define IDX2F(i,j,ld) ((((j)-1)*(ld))+((i)-1))
subroutine modify ( devPtrM, ldm, n, p, q, alpha, beta )
implicit none
integer sizeof_real
parameter (sizeof_real=4)
integer ldm, n, p, q
#if ARCH_64
integer*8 devPtrM
#else
integer*4 devPtrM
#endif
real*4 alpha, beta
call cublas_sscal ( n-p+1, alpha,
1 devPtrM+IDX2F(p, q, ldm)*sizeof_real,
2 ldm)
call cublas_sscal(ldm-p+1, beta,
1 devPtrM+IDX2F(p, q, ldm)*sizeof_real,
2 1)
return
end
program matrixmod
implicit none
integer M,N,sizeof_real
#if ARCH_64
integer*8 devPtrA
#else
integer*4 devPtrA
#endif
parameter(M=6,N=5,sizeof_real=4)
real*4 a(M,N)
integer i,j,stat
external cublas_init, cublas_set_matrix, cublas_get_matrix
external cublas_shutdown, cublas_alloc
integer cublas_alloc, cublas_set_matrix, cublas_get_matrix
do j=1,N
do i=1,M
a(i,j)=(i-1)*M+j
enddo
enddo
call cublas_init
stat= cublas_alloc(M*N, sizeof_real, devPtrA)
if (stat.NE.0) then
write(*,*) "device memory allocation failed"
call cublas_shutdown
stop
endif
stat = cublas_set_matrix(M,N,sizeof_real,a,M,devPtrA,M)
if (stat.NE.0) then
call cublas_free( devPtrA )
write(*,*) "data download failed"
call cublas_shutdown
stop
endif
—
— Code block continues below. Space added for formatting purposes. —
—
call modify(devPtrA, M, N, 2, 3, 16.0, 12.0)
stat = cublas_get_matrix(M, N, sizeof_real, devPtrA, M, a, M )
if (stat.NE.0) then
call cublas_free ( devPtrA )
write(*,*) "data upload failed"
call cublas_shutdown
stop
endif
call cublas_free ( devPtrA )
call cublas_shutdown
do j = 1 , N
do i = 1 , M
write (*,"(F7.0$)") a(i,j)
enddo
write (*,*) ""
enddo
stop
end
8. Interaction with Other Libraries and Tools
This section describes important requirements and recommendations that ensure correct use of cuBLAS with other libraries and utilities.
8.1. nvprune
nvprune enables pruning relocatable host objects and static libraries to only contain device code for the specific target architectures. In case of cuBLAS, particular care must be taken if using nvprune with compute capabilities, whose minor revision number is different than 0. To reduce binary size, cuBLAS may only store major revision equivalents of CUDA binary files for kernels reused between different minor revision versions. Therefore, to ensure that a pruned library does not fail for arbitrary problems, the user must keep binaries for a selected architecture and all prior minor architectures in its major architecture.
For example, the following call prunes libcublas_static.a to contain only sm_75 (Turing) and sm_70 (Volta) cubins:
nvprune --generate-code code=sm_70 --generate-code code=sm_75 libcublasLt_static.a -o libcublasLt_static_sm70_sm75.a
which should be used instead of:
nvprune -arch=sm_75 libcublasLt_static.a -o libcublasLt_static_sm75.a
9. Acknowledgements
NVIDIA would like to thank the following individuals and institutions for their contributions:
Portions of the SGEMM, DGEMM, CGEMM and ZGEMM library routines were written by Vasily Volkov of the University of California.
Portions of the SGEMM, DGEMM and ZGEMM library routines were written by Davide Barbieri of the University of Rome Tor Vergata.
Portions of the DGEMM and SGEMM library routines optimized for Fermi architecture were developed by the University of Tennessee. Subsequently, several other routines that are optimized for the Fermi architecture have been derived from these initial DGEMM and SGEMM implementations.
The substantial optimizations of the STRSV, DTRSV, CTRSV and ZTRSV library routines were developed by Jonathan Hogg of The Science and Technology Facilities Council (STFC). Subsequently, some optimizations of the STRSM, DTRSM, CTRSM and ZTRSM have been derived from these TRSV implementations.
Substantial optimizations of the SYMV and HEMV library routines were developed by Ahmad Abdelfattah, David Keyes and Hatem Ltaief of King Abdullah University of Science and Technology (KAUST).
Substantial optimizations of the TRMM and TRSM library routines were developed by Ali Charara, David Keyes and Hatem Ltaief of King Abdullah University of Science and Technology (KAUST).
This product includes {fmt} - A modern formatting library https://fmt.devCopyright (c) 2012 - present, Victor Zverovich.
This product includes spdlog - Fast C++ logging library. https://github.com/gabime/spdlog The MIT License (MIT).
This product includes SIMD Library for Evaluating Elementary Functions, vectorized libm and DFT https://sleef.orgBoost Software License - Version 1.0 - August 17th, 2003.
This product includes Frozen - a header-only, constexpr alternative to gperf for C++14 users. https://github.com/serge-sans-paille/frozen Apache License - Version 2.0, January 2004.
This product includes Boost C++ Libraries - free peer-reviewed portable C++ source libraries https://www.boost.org/ Boost Software License - Version 1.0 - August 17th, 2003.
This product includes Zstandard - a fast lossless compression algorithm, targeting real-time compression scenarios at zlib-level and better compression ratios. https://github.com/facebook/zstd The BSD License.
10. Notices
10.1. Notice
This document is provided for information purposes only and shall not be regarded as a warranty of a certain functionality, condition, or quality of a product. NVIDIA Corporation (“NVIDIA”) makes no representations or warranties, expressed or implied, as to the accuracy or completeness of the information contained in this document and assumes no responsibility for any errors contained herein. NVIDIA shall have no liability for the consequences or use of such information or for any infringement of patents or other rights of third parties that may result from its use. This document is not a commitment to develop, release, or deliver any Material (defined below), code, or functionality.
NVIDIA reserves the right to make corrections, modifications, enhancements, improvements, and any other changes to this document, at any time without notice.
Customer should obtain the latest relevant information before placing orders and should verify that such information is current and complete.
NVIDIA products are sold subject to the NVIDIA standard terms and conditions of sale supplied at the time of order acknowledgement, unless otherwise agreed in an individual sales agreement signed by authorized representatives of NVIDIA and customer (“Terms of Sale”). NVIDIA hereby expressly objects to applying any customer general terms and conditions with regards to the purchase of the NVIDIA product referenced in this document. No contractual obligations are formed either directly or indirectly by this document.
NVIDIA products are not designed, authorized, or warranted to be suitable for use in medical, military, aircraft, space, or life support equipment, nor in applications where failure or malfunction of the NVIDIA product can reasonably be expected to result in personal injury, death, or property or environmental damage. NVIDIA accepts no liability for inclusion and/or use of NVIDIA products in such equipment or applications and therefore such inclusion and/or use is at customer’s own risk.
NVIDIA makes no representation or warranty that products based on this document will be suitable for any specified use. Testing of all parameters of each product is not necessarily performed by NVIDIA. It is customer’s sole responsibility to evaluate and determine the applicability of any information contained in this document, ensure the product is suitable and fit for the application planned by customer, and perform the necessary testing for the application in order to avoid a default of the application or the product. Weaknesses in customer’s product designs may affect the quality and reliability of the NVIDIA product and may result in additional or different conditions and/or requirements beyond those contained in this document. NVIDIA accepts no liability related to any default, damage, costs, or problem which may be based on or attributable to: (i) the use of the NVIDIA product in any manner that is contrary to this document or (ii) customer product designs.
No license, either expressed or implied, is granted under any NVIDIA patent right, copyright, or other NVIDIA intellectual property right under this document. Information published by NVIDIA regarding third-party products or services does not constitute a license from NVIDIA to use such products or services or a warranty or endorsement thereof. Use of such information may require a license from a third party under the patents or other intellectual property rights of the third party, or a license from NVIDIA under the patents or other intellectual property rights of NVIDIA.
Reproduction of information in this document is permissible only if approved in advance by NVIDIA in writing, reproduced without alteration and in full compliance with all applicable export laws and regulations, and accompanied by all associated conditions, limitations, and notices.
THIS DOCUMENT AND ALL NVIDIA DESIGN SPECIFICATIONS, REFERENCE BOARDS, FILES, DRAWINGS, DIAGNOSTICS, LISTS, AND OTHER DOCUMENTS (TOGETHER AND SEPARATELY, “MATERIALS”) ARE BEING PROVIDED “AS IS.” NVIDIA MAKES NO WARRANTIES, EXPRESSED, IMPLIED, STATUTORY, OR OTHERWISE WITH RESPECT TO THE MATERIALS, AND EXPRESSLY DISCLAIMS ALL IMPLIED WARRANTIES OF NONINFRINGEMENT, MERCHANTABILITY, AND FITNESS FOR A PARTICULAR PURPOSE. TO THE EXTENT NOT PROHIBITED BY LAW, IN NO EVENT WILL NVIDIA BE LIABLE FOR ANY DAMAGES, INCLUDING WITHOUT LIMITATION ANY DIRECT, INDIRECT, SPECIAL, INCIDENTAL, PUNITIVE, OR CONSEQUENTIAL DAMAGES, HOWEVER CAUSED AND REGARDLESS OF THE THEORY OF LIABILITY, ARISING OUT OF ANY USE OF THIS DOCUMENT, EVEN IF NVIDIA HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. Notwithstanding any damages that customer might incur for any reason whatsoever, NVIDIA’s aggregate and cumulative liability towards customer for the products described herein shall be limited in accordance with the Terms of Sale for the product.
10.2. OpenCL
OpenCL is a trademark of Apple Inc. used under license to the Khronos Group Inc.
10.3. Trademarks
NVIDIA and the NVIDIA logo are trademarks or registered trademarks of NVIDIA Corporation in the U.S. and other countries. Other company and product names may be trademarks of the respective companies with which they are associated.